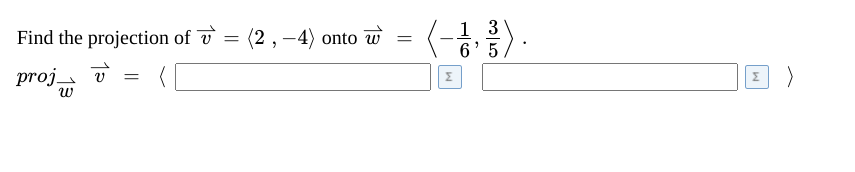Home /
Expert Answers /
Precalculus /
find-the-projection-of-vec-v-langle-2-4-rangle-onto-vec-w-left-langle-frac-1-6-pa697
(Solved): Find the projection of \( \vec{v}=\langle 2,-4\rangle \) onto \( \vec{w}=\left\langle-\frac{1}{6}, ...
Find the projection of \( \vec{v}=\langle 2,-4\rangle \) onto \( \vec{w}=\left\langle-\frac{1}{6}, \frac{3}{5}\right\rangle \). \( \operatorname{proj}_{\vec{w}} \vec{v}=\langle \) \( \Sigma\rangle \)
Expert Answer
The given vectors are:- v?= < 2, ?4 > w?= < ?16, 35 > The dot product of two vectors is:- w?.v?=(?16)(2)+(35)(?4) w?.v?=?13?125 w?.v?=?515?3615 w?.v?=