(Solved): Find the volume \( V \) of the described solid \( S \). A right circular cone with height \( 4 h \ ...

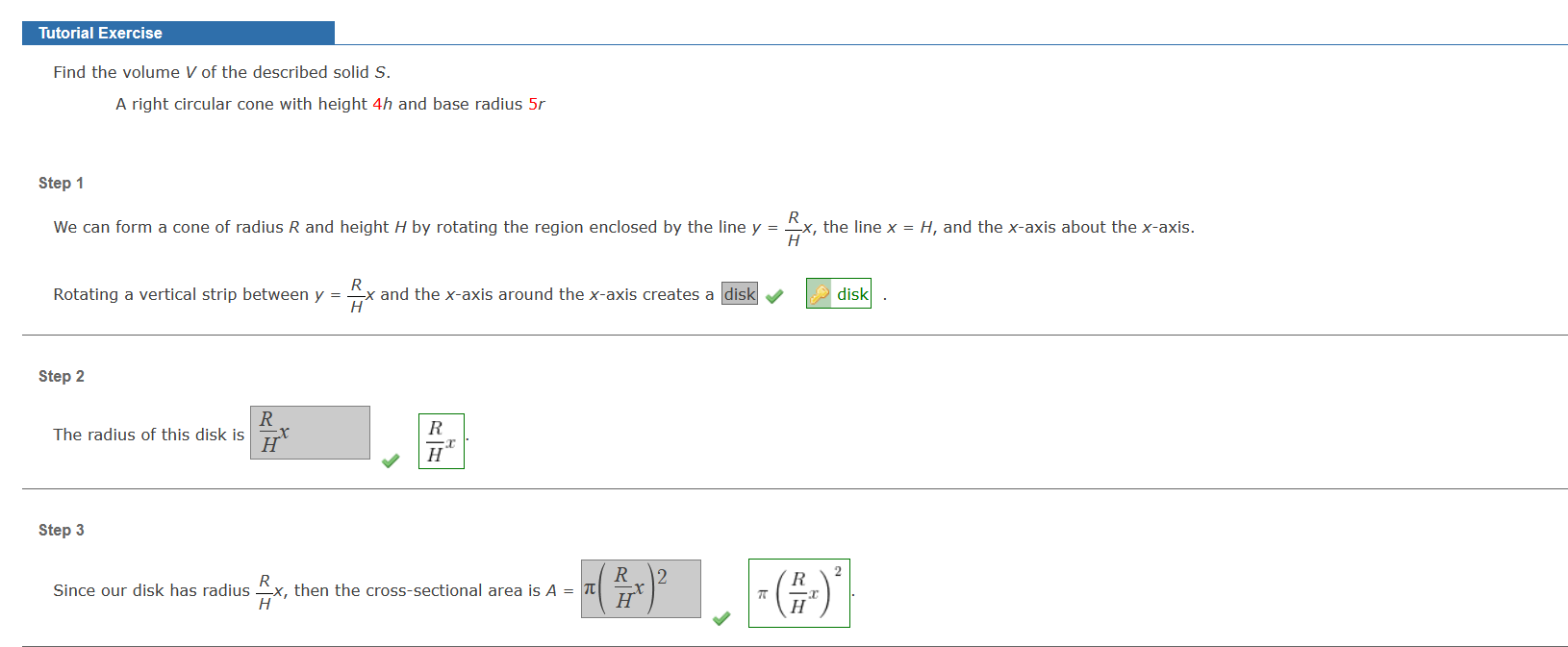
Find the volume \( V \) of the described solid \( S \). A right circular cone with height \( 4 h \) and base radius \( 5 r \) Step 1 We can form a cone of radius \( R \) and height \( H \) by rotating the region enclosed by the line \( y=\frac{R}{H} x \), the line \( x=H \), and the \( x \)-axis about the Rotating a vertical strip between \( y=\frac{R}{H} x \) and the \( x \)-axis around the \( x \)-axis creates a Step 2 The radius of this disk is Step 3 Since our disk has radius \( \frac{R}{H} x \), then the cross-sectional area is \( A=\pi\left(\frac{R}{H} x\right)^{2} \pi\left(\frac{R}{H}\right)^{2} \). Since our disk has radius \( \frac{R}{H} x \), then the cross-sectional area is \( A=\pi\left(\frac{R}{H} x\right)^{2} \pi\left(\frac{R}{H} x\right)^{2} \). Step 4 Now we can say that the volume of the solid created by rotating the region around the \( x \)-axis is \( V=\int_{x_{1}}^{x_{2}} A(x) d x=\int_{0}^{H} \pi\left(\frac{R}{H} x\right)^{2} d x \). Step 5 So, the volume of our solid is \( \pi \) ]\( _{0}^{H}=\frac{H^{3}}{3}-\frac{0^{3}}{3} \) . Let \( R=5 r \) and \( H=4 h \). Therefore the volume \( V \) of this solid is