(Solved): For the functions \( f(t)=e^{t} \) and \( g(t)=e^{-4 t} \), defined on \( 0 \leq t ...

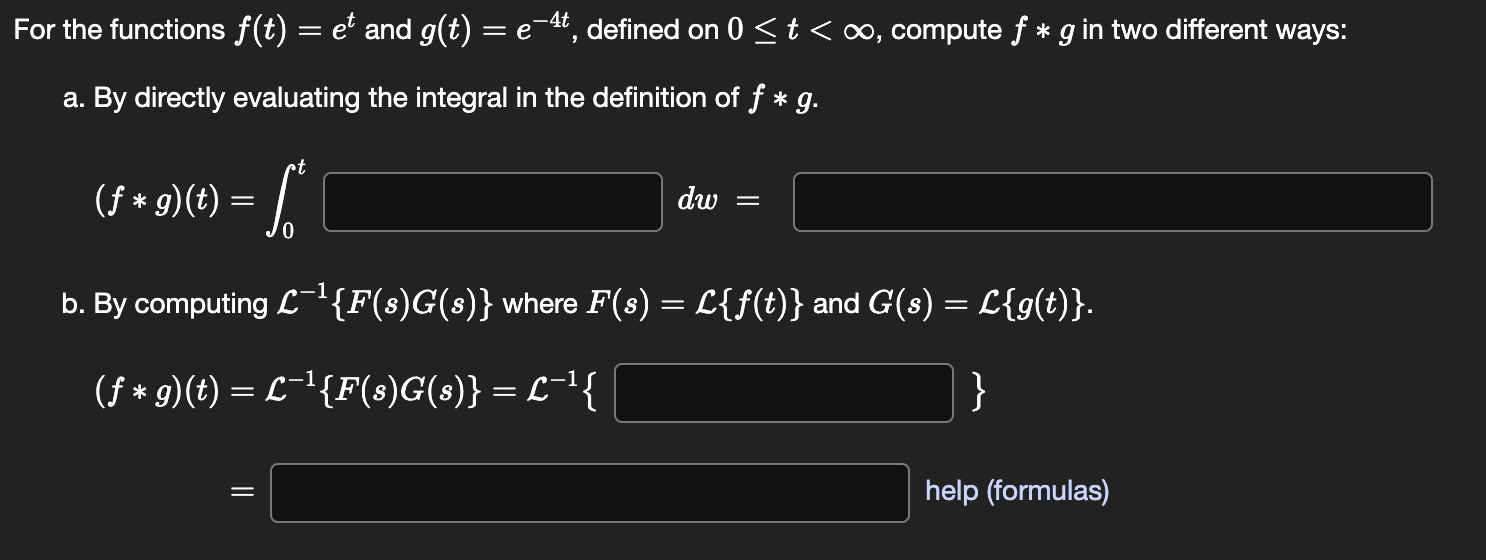
For the functions \( f(t)=e^{t} \) and \( g(t)=e^{-4 t} \), defined on \( 0 \leq t<\infty \), compute \( f * g \) in two different ways: a. By directly evaluating the integral in the definition of \( f * g \). \[ (f * g)(t)=\int_{0}^{t} \quad d w= \] b. By computing \( \mathcal{L}^{-1}\{F(s) G(s)\} \) where \( F(s)=\mathcal{L}\{f(t)\} \) and \( G(s)=\mathcal{L}\{g(t)\} \). \[ \begin{aligned} (f * g)(t) &=\mathcal{L}^{-1}\{F(s) G(s)\}=\mathcal{L}^{-1}\{\\ &= \end{aligned} \]