Home /
Expert Answers /
Mechanical Engineering /
for-the-system-shown-derive-equations-of-motion-and-find-the-natural-frequencies-the-eigen-modes-pa246
(Solved): For the system shown, derive equations of motion, and find the natural frequencies, the eigen modes ...
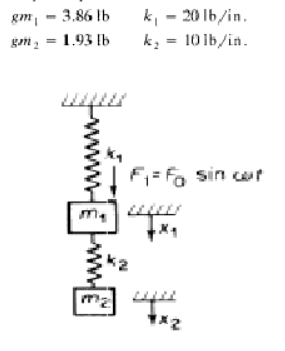
For the system shown, derive equations of motion, and find the natural frequencies, the eigen modes and the amplitudes of displacements under zero initial conditions as functions of frequency of external force ????.
gm1= 3.86 lb
gm2 =1.93 lb
k1= 20 lb/in
k2= 10 lb/in
Expert Answer
To derive the equations of motion for the given system, let's assume the displacements of masses m1 and m2 from their respective equilibrium positions as x1 and x2, respectively. Also, let's assume that the external force is applied to mass m1. The equation of motion for mass m1 can be written as: The equation of motion for mass m2 can be written as: To simplify the equations, we can convert the given masses from pounds to slugs (1 slug = 32.2 lb?s²/ft) and convert the spring constants from lb/in to lb/s². Let's perform these conversions: = 0.62 lb/s² Now, let's rewrite the equations of motion with the converted values: Equation of motion for mass m1: 0.12 * x1'' + 0.62 * x1 + 0.31 * (x1 - x2) = F * sin(?t) Equation of motion for mass m2: To solve these equations, we can rearrange them in matrix form: [-0.31 0.06] [x2''] = [0.31 * x1 - 0.06 * x2]