(Solved): For this problem, camy at least four digits after the decimal in your calculations. Answers may va ...

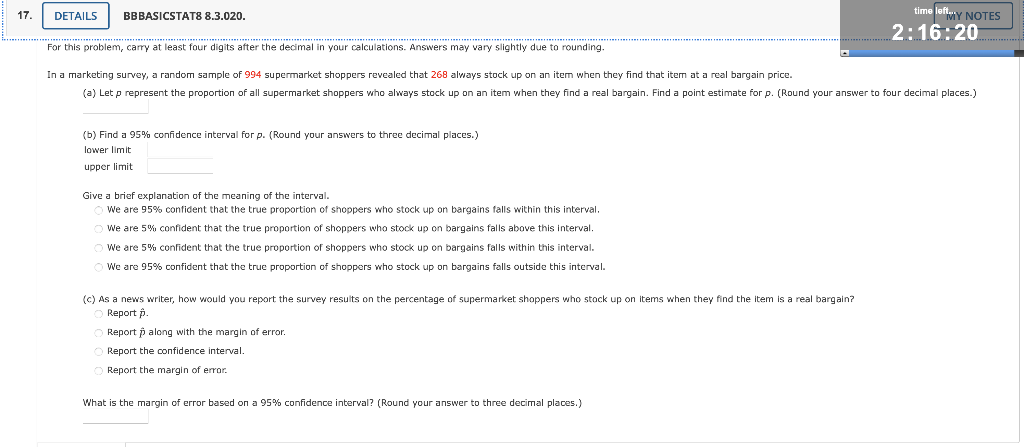
For this problem, camy at least four digits after the decimal in your calculations. Answers may vary slightly due to rounding. In a marketing survey, a random sample of 994 supermarket shoppers revealed that 268 always stock up on an item when they find that item at a real bargain price. (b) Find a $95\%$ confidence interval for p. (Round your answers to three decimal places.) lower limit upper limit Give a brief explanation of the meaning of the interval. We are $95\%$ confident that the true proportion of shoppers who stock up on bargains falls within this interval. We are $5\%$ confident that the true proportion of shoppers who stock up on bargains falls above this interval. We are $5\%$ confident that the true proportion of shoppers who stock up on bargains falls within this interval. We are $95\%$ confident that the true proportion of shoppers who stock up on bargains falls outside this interval. (c) As a news writer, how would you report the survey results on the percentage of supermarket shoppers who stock up on items when they find the item is a real bargain? Report $\hat{p}$. Report $\hat{p}$ along with the margin of error. Report the confidence interval. Report the margin of error. What is the margin of error based on a $95\%$ confidence interval? (Round your answer to three decimal places.)