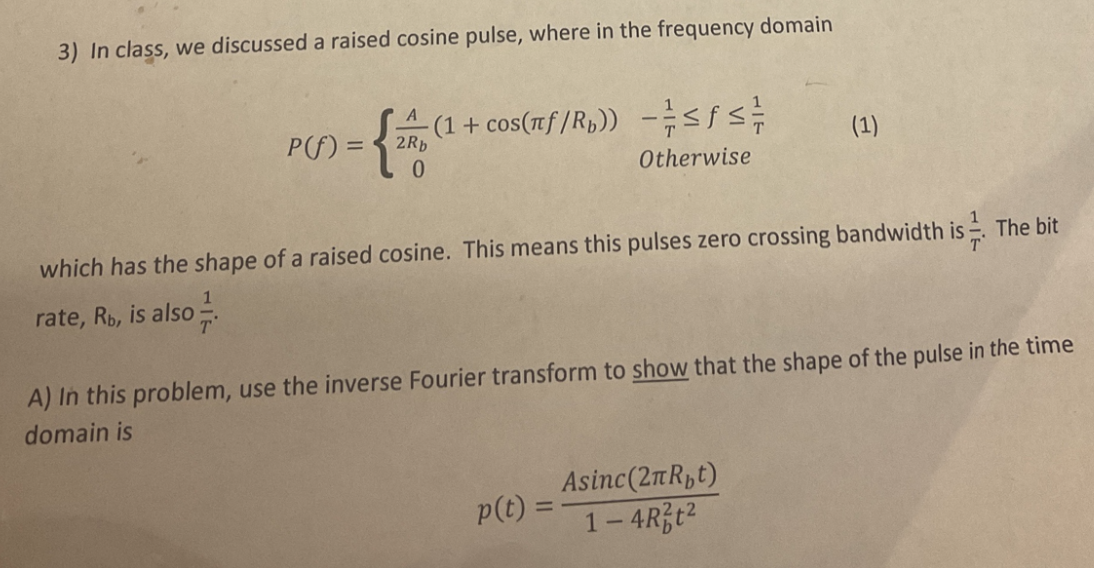(Solved): Fourier Transform with Digital and analog communication system problem Please answer all of the ques ...

Fourier Transform with Digital and analog communication system problem

Please answer all of the questions with steps otherwise do not answer at all.

I suck at this stuff...

 

 

3) In class, we discussed a raised cosine pulse, where in the frequency domain \[ P(f)=\left\{\begin{array}{ll} \frac{A}{2 R_{b}}\left(1+\cos \left(\pi f / R_{b}\right)\right) & -\frac{1}{T} \leq f \leq \frac{1}{T} \\ 0 & \text { Otherwise } \end{array}\right. \] which has the shape of a raised cosine. This means this pulses zero crossing bandwidth is \( \frac{1}{T} \). The bit rate, \( \mathrm{R}_{\mathrm{b}} \), is also \( \frac{1}{T} \) A) In this problem, use the inverse Fourier transform to show that the shape of the pulse in the time domain is \[ p(t)=\frac{A \operatorname{sinc}\left(2 \pi R_{b} t\right)}{1-4 R_{b}^{2} t^{2}} \] TABLE \( 3.1 \) Short Table of Fourier Transforms