(Solved): HW21 eigenspaces diagonalization: Problem 7 (1 point) Let A=[2057] Find a matrix S, ...

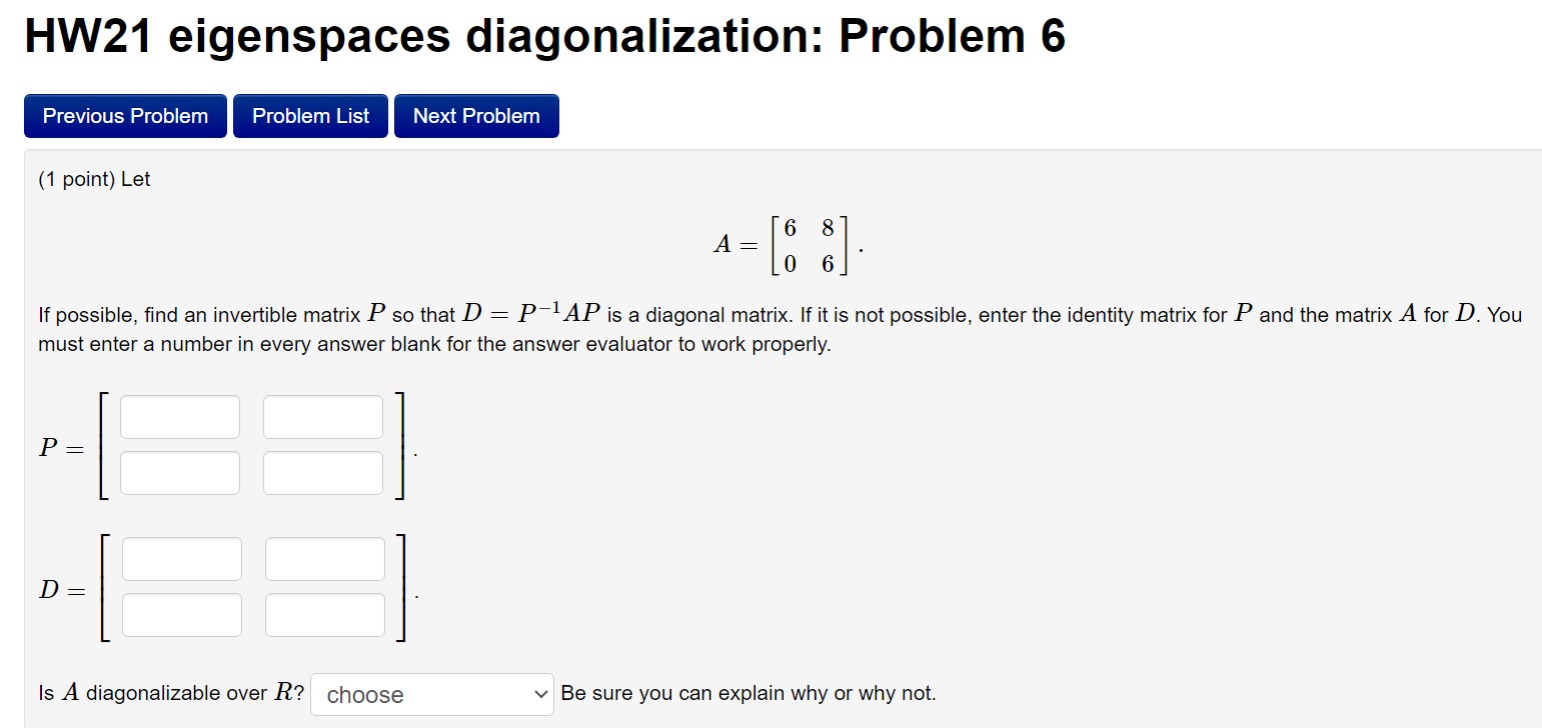
HW21 eigenspaces diagonalization: Problem 7 (1 point) Let $A=\left[\begin{array}{cc}-2& -5\\ 0& -7\end{array}\right]$ Find a matrix $S$, a diagonal matrix $D$ and $S^{-1}$ such that $A=SD{S}^{-1}$. $S=[],D=[],S^{-1}=[]$ HW21 eigenspaces diagonalization: Problem 6 (1 point) Let $A=\left[\begin{array}{ll}6& 8\\ 0& 6\end{array}\right].$ If possible, find an invertible matrix $P$ so that $D=P^{-1}AP$ is a diagonal matrix. If it is not possible, enter the identity matrix for $P$ and the matrix $A$ for $D$. You must enter a number in every answer blank for the answer evaluator to work properly. $\begin{array}{l}P=\left[\begin{array}{l}l\end{array}\right]\text{. }\\ D=\left[\begin{array}{l}\text{ ] }\end{array}\right]\end{array}$ Is $A$ diagonalizable over $R$ ? Be sure you can explain why or why not. 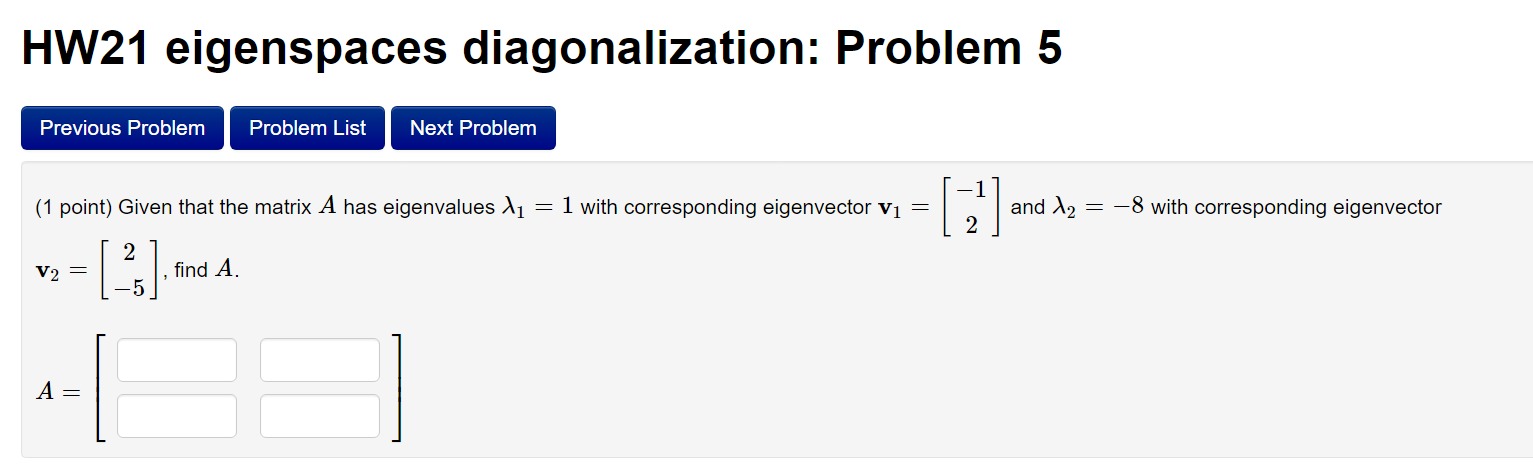HW21 eigenspaces diagonalization: Problem 5 (1 point) Given that the matrix $A$ has eigenvalues ${\lambda }_1=1$ with corresponding eigenvector ${\mathbf{v}}_1=\left[\begin{array}{c}-1\\ 2\end{array}\right]$ and ${\lambda }_2=-8$ with corresponding eigenvector ${\mathbf{v}}_2=\left[\begin{array}{c}2\\ -5\end{array}\right]$, find $A$ $A=[]$