(Solved): i can't sure below answer is correct so give me real solution to this problem please  i want re ...

i can't sure below answer is correct so give me real solution to this problem please 
i want real answer 
 

 

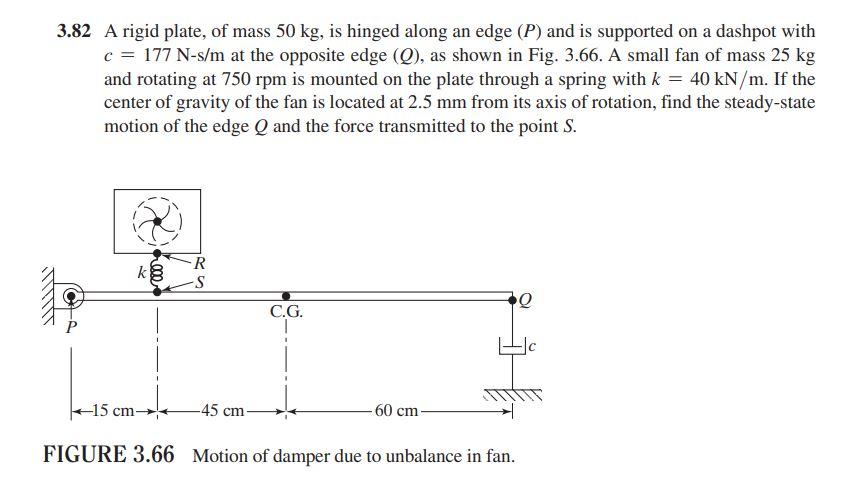
3.82 A rigid plate, of mass 50 kg, is hinged along an edge (P) and is supported on a dashpot with c = 177 N-s/m at the opposite edge (Q), as shown in Fig. 3.66. A small fan of mass 25 kg and rotating at 750 rpm is mounted on the plate through a spring with k = 40 kN/m. If the center of gravity of the fan is located at 2.5 mm from its axis of rotation, find the steady-state motion of the edge Q and the force transmitted to the point S. R -S Q C.G. -15 cm- -45 cm- 60 cm FIGURE 3.66 Motion of damper due to unbalance in fan. k •000* 177 (2)(25) (40) = 0,088 5 r = 1.96 = r² = 3.84 and = tan 25r 1-r² =tan(-0.11) = -6.27° Steady state motion of Q = ? (1.2) = 0.0084 cos (78.54 t + 6.27) m Displacement of S=? (0.15) mm = 1.005 mm Max deformation of spring? 0.003 m Max. force transmitted to point S = 40000 (0.003) = 120 N k 3.82) 40000 = 40 rad/s m 25 Weight of plate= 50 x 9.81 490.5 N Weight of fan = 25 x 9.81 = 245.25 N (Jp)phen(490.5) (1.2) + (245.25) (0.15)² = 240.95 Nm 3 750 x 27 F? = meo² = (25) (0.0025) = 385.6 N 60 ? = 78.54 rad/s r = 1.96 r² = 3.84 Point R is subjected to the force F(t) = F, cos ax F(t) = 356.6 cos 78.54t N Assume that S is not moving. Then R is displaced by: F cos cot F, cos cot 385.6 cos 78.54t x(t) = k-mo 40000(1-3.84) 4-(2 0 or x(t) = 0.003 cos 78.54 t meters Let = angular displacement of plate PQ. Displacement of S= 0.150 metres Extension of spring RS = (0.15 0-0.003 cos 78.54t) m Restoring moment of spring force about P = (40000) (0.15 0 -0.003 cos 78.54t) (0.15) Nm Velocity of Q = 1.20 m/s DAMPING force at Q=1.20 (177)=212.40 N Moment of damping force about P = (1.2)212.40=254.80N Equation of motion of plate PQ: J0+254.80 + 6000(0.15-0.003 cos 78.54t) = 64.370 +254.80 +9000 = 18 cos 78.54t El Comparing (El) with Eq (3.24), the solution of (E1) can be expressed as 0 (t) = H cos(@t-Ø) Where, from Eqs (3.30) and (3.31), we get 80 900 O= = 0.007 rad ((1. 1-3.84)²+(2(0.08) (1.96)))* -R ca 15 cm 45 cm 60 cm ithink this is wrong