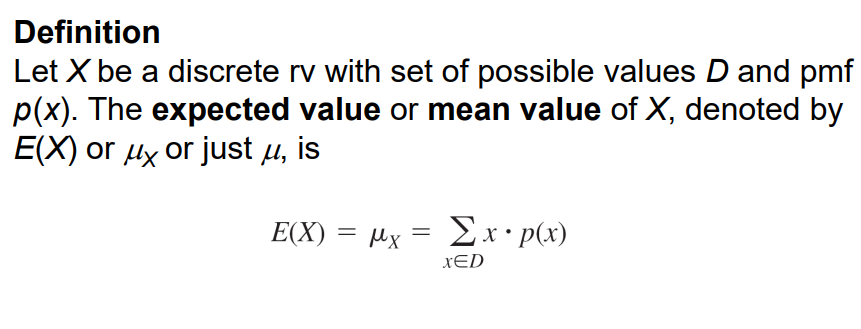(Solved): If I have a piecewise probability mass function, p(x), which is 1/9 when x= 0 1/x(x+1) when x i ...

If I have a piecewise probability mass function, p(x), which is

1/9 when x= 0

1/x(x+1) when x is between 1,2, 3, ...., 8.

The question says:

The entropy of a random variable represents the amount of information in the variable. For a discrete random variable the entropy is given by -E(ln(p(x))). Calculate the entropy of X.

I'm reading this as "negative (the expected value of (the natural logarithm of p(x)))".

The standard expected value formula is in the picture attached. ? x * p(x)

Now how do I have to change that formula to calculate  -E(ln(p(x))).

My idea is that its ? x * ln(p(x)). 

Can someone confirm this and tell me what they get for their entropy?