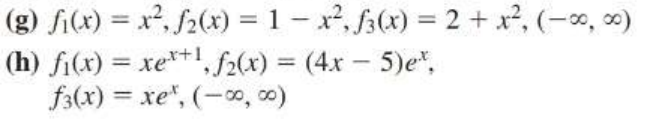Home /
Expert Answers /
Calculus /
in-each-case-a-to-h-determine-whether-the-given-set-of-functions-f1-f2-and-also-f1-f2-f3-pa355
(Solved): In each case (a) to (h), determine whether the given set of functions {f1, f2} and also {f1, f2, f3} ...
In each case (a) to (h), determine whether the given set of functions {f1, f2} and also {f1, f2, f3} is linearly Independent. ‘Y’ for
independent and ‘N’ for not independent.
(g) \( f_{1}(x)=x^{2}, f_{2}(x)=1-x^{2}, f_{3}(x)=2+x^{2},(-\infty, \infty \) (h) \( f_{1}(x)=x e^{x+1}, f_{2}(x)=(4 x-5) e^{x} \), \( f_{3}(x)=x e^{x},(-\infty, \infty) \)
Expert Answer
(g). Given functions are f1(x)=x2,f2(x)=1?x2andf3(x)=2+x2 Now if f1(x)andf2(x) are linearly independent then af1(x)+bf2(x)=0, implies that a=b=0, othe