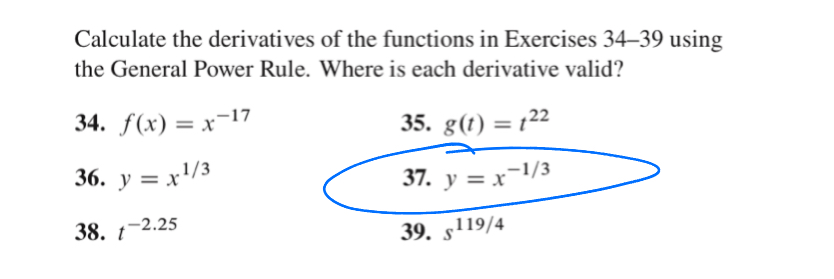(Solved): In Exercises 40-50, you may use the formulas for derivatives Calculate the derivatives of the funct ...
In Exercises 40-50, you may use the formulas for derivatives Calculate the derivatives of the functions in Exercises 34-39 using the General Power Rule. Where is each derivative valid?
f(x)=x^(-17)
g(t)=t^(22)
y=x^((1)/(3))
y=x^(-(1)/(3))
t^(-2.25)
s^((119)/(4))In Exercises 1-12, find an equation of the straight line tangent to the given curve at the point indicated.
y=3x-1at
(1,2)
y=(x)/(2)at
(a,(a)/(2))
y=2x^(2)-5at
(2,3)
y=6-x-x^(2)at
x=-2
y=x^(3)+8at
x=-2
y=(1)/(x^(2)+1)at
(0,1)
y=\sqrt(x+1)at
x=3
y=(1)/(\sqrt(x))at
x=9
y=(2x)/(x+2)at
x=2
y=\sqrt(5-x^(2))at
x=1
y=x^(2)at
x=x_(0)
y=(1)/(x)at
(a,(1)/(a))Find all points on the curve
y=x^(3)-x+1where the tangent line is parallel to the line
y=2x+5. Find all points on the curve
y=(1)/(x)where the tangent line is perpendicular to the line
y=4x-3. For what value of the constant
kis the line
x+y=knormal to the curve
y=x^(2)? For what value of the constant
kdo the curves
y=kx^(2)and
y=k(x-2)^(2)intersect at right angles? Hint: Where do the curves intersect? What are their slopes there? Use a graphics utility to plot the following curves. Where does the curve have a horizontal tangent? Does the curve fail to have a tangent line anywhere?
y=x^(3)(5-x)^(2)
y=2x^(3)-3x^(2)-12x+1established in this section. Calculate
(d)/(ds)\sqrt(s)|_(s)=9. Find
F^(')((1)/(4))if
F(x)=(1)/(x). Find
f^(')(8)if
f(x)=x^(-(2)/(3)). Find
d(y)/(d)t|_(t)=4if
y=t^((1)/(4)). Find an equation of the straight line tangent to the curve
y=\sqrt(x)at
x=x_(0). Find an equation of the straight line normal to the curve
y=(1)/(x)at the point where
x=a. Show that the curve
y=x^(2)and the straight line
x+4y=18intersect at right angles at one of their two intersection points. Hint: Find the product of their slopes at their intersection points. There are two distinct straight lines that pass through the point
(1,-3)and are tangent to the curve
y=x^(2). Find their equations. Hint: Draw a sketch. The points of tangency are not given; let them be denoted
(a,a^(2)). Find equations of two straight lines that have slope -2 and are tangent to the graph of
y=(1)/(x). Find the slope of a straight line that passes through the point
(-2,0)and is tangent to the curve
y=\sqrt(x).