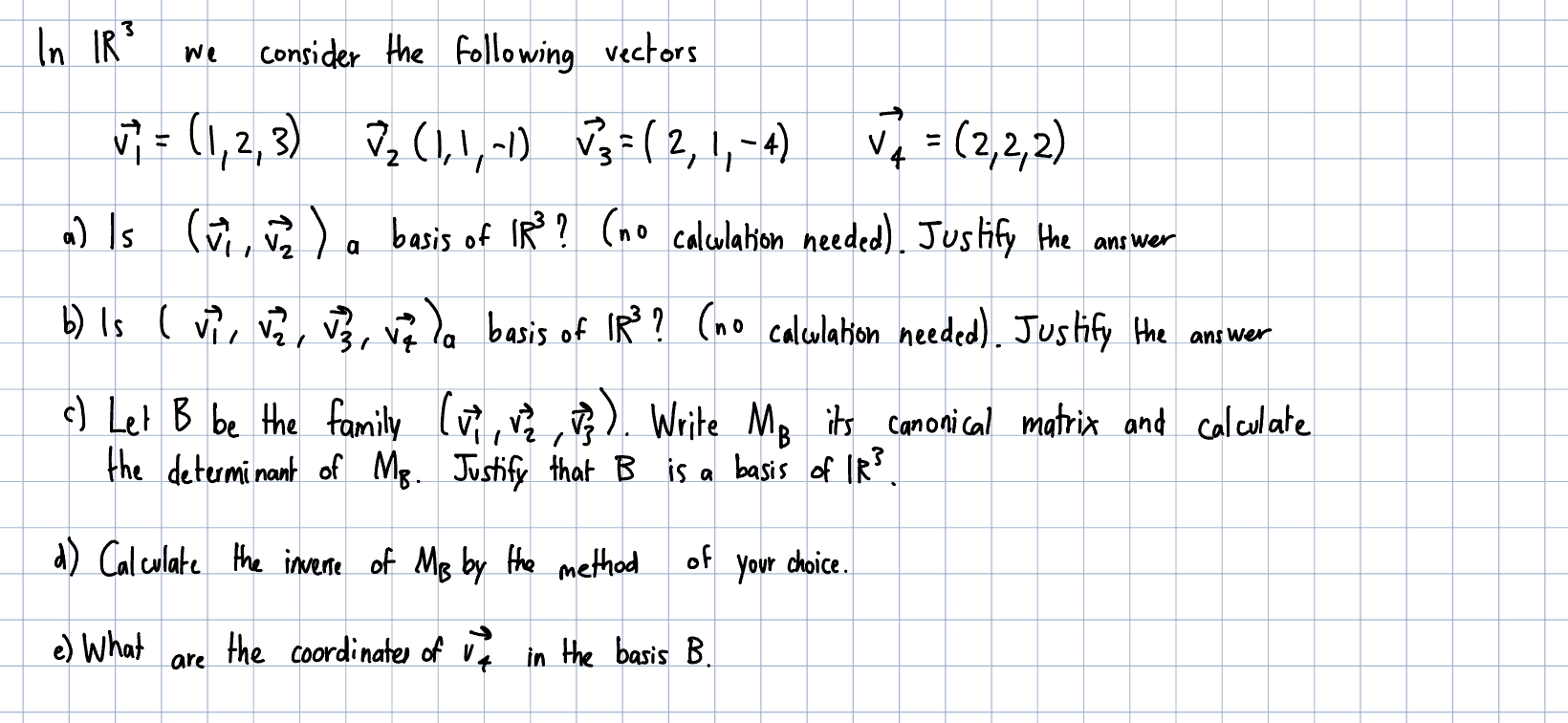Home /
Expert Answers /
Advanced Math /
in-r-3-we-consider-the-following-vectors-vec-v-1-1-2-3-vec-v-2-1-1-1-vec-v-3-2-1-4-pa551
(Solved): In R^(3) we consider the following vectors vec(v)_(1)=(1,2,3),vec(v)_(2)(1,1,-1),vec(v)_(3)=(2,1,-4) ...
In
R^(3)we consider the following vectors
vec(v)_(1)=(1,2,3),vec(v)_(2)(1,1,-1),vec(v)_(3)=(2,1,-4),vec(v)_(4)=(2,2,2)a) Is
(vec(v)_(1),vec(v)_(2))a basis of
R^(3)? (no calculation needed). Justify the answer b) Is
(vec(v_(1)),vec(v_(2)),vec(v_(3)),vec(v_(4)))_(a )basis of
R^(3)? (no calculation needed). Justify the answer c) Let
Bbe the family
(vec(v)_(1),vec(v)_(2),vec(v)_(3)). Write
M_(B)its canonical matrix and calculate the determinant of
M_(B). Justify that
Bis a basis of
R^(3). d) Calculate the imvere of
M_(B)by the method of your choice. e) What are the coordinater of
vec(v)_(uarr)in the basis
B.