Home /
Expert Answers /
Advanced Math /
it-39-s-linear-algebra-question-plz-do-steps-by-steps-question-let-k-be-a-field-n-n-suppose-the-pa517
(Solved): it's linear algebra question plz do steps by steps Question: Let K be a field n N. Suppose the ...
it's linear algebra question plz do steps by steps
Question: Let K be a field n ∈ N. Suppose the vector space Pn ≤ K[x] with a basis of Bn :=
{1, x, x2
, . . . , xn}. Let a0, a1, . . . , an ∈ K with ai unequal to aj. The function is defined as Φ: Pn → Kn+1, f → (f(a0), f(a1), ..., f(an)). Find for the elements a0, a1, a2, a3 the transformation matrix AΦBS4 with basis B3 of P3 and S4 as the standard basis of K4.
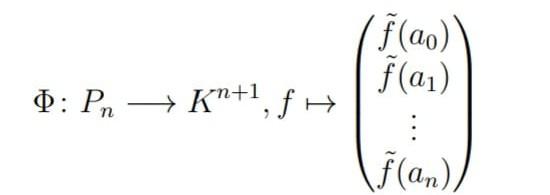
if you don't know give to someone else but don't do wrong
Expert Answer
To find the transformation matrix A with respect to the given bases, we need to determine the coordinates of the images of the basis vectors of P3 under the linear transformation defined by f.Let's start by considering the first basis vector of P3, which is (1, 0, 0, 0) in S4. The image of this vector under f is (f(a0), f(a1), f(a2), f(a3)). To find the coordinates of this image vector with respect to B3, we need to express it as a linear combination of the basis vectors of B3.Since the first coordinate of the image vector is f(a0), which is the value of the function f at a0, we can write:f(a0) = c0(1) + c1(x) + c2(x^2) + c3(x^3)for some constants c0, c1, c2, and c3. Similarly, we can write:f(a1) = d0(1) + d1(x) + d2(x^2) + d3(x^3)f(a2) = e0(1) + e1(x) + e2(x^2) + e3(x^3)f(a3) = g0(1) + g1(x) + g2(x^2) + g3(x^3)for some constants d0, d1, d2, d3, e0, e1, e2, e3, g0, g1, g2, and g3.Substituting these expressions into the image vector, we get:(f(a0), f(a1), f(a2), f(a3)) = (c0, d0, e0, g0) + (c1, d1, e1, g1)x + (c2, d2, e2, g2)x^2 + (c3, d3, e3, g3)x^3