Home /
Expert Answers /
Mechanical Engineering /
learning-goal-to-use-the-principle-of-work-and-energy-to-calculate-the-work-done-by-springs-gravi-pa966
(Solved): Learning Goal: To use the Principle of Work and Energy to calculate the work done by springs, gravi ...


Learning Goal: To use the Principle of Work and Energy to calculate the work done by springs, gravity, and friction forces. This Principle of Work and Energy is expressed by the following equation: Or, to summarize in words, the initial translational and rotational kinetic energy of a rigid body plus the work done by all the external forces and couple moments acting on the body as it moves from the initial to the final configuration is equal to the final total kinetic energy of the body. Figure 1 of 4
Learning Goal: To use the Principle of Work and Energy to calculate the work done by springs, gravity, and friction forces. This Principle of Work and Energy is expressed by the following equation: Or, to summarize in words, the initial translational and rotational kinetic energy of a rigid body plus the work done by all the external forces and couple moments acting on the body as it moves from the initial to the final configuration is equal to the final total kinetic energy of the body. igure 2 of 4
Figure 4 of 4 Next Figure
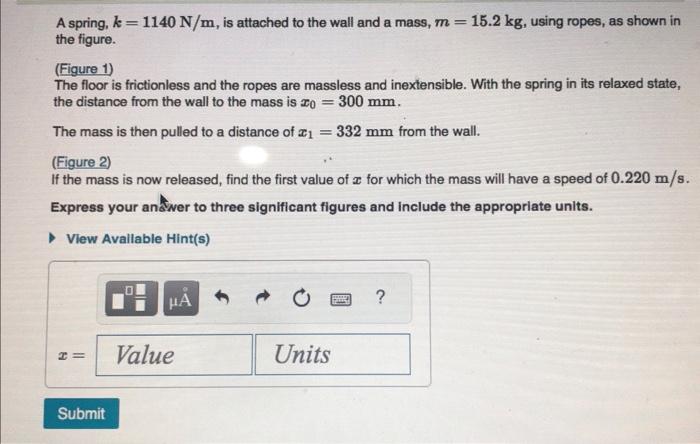
A spring, , is attached to the wall and a mass, , using ropes, as shown in the figure. (Figure 1) The floor is frictionless and the ropes are massless and inextensible. With the spring in its relaxed state, the distance from the wall to the mass is . The mass is then pulled to a distance of from the wall. (Figure 2) If the mass is now released, find the first value of for which the mass will have a speed of . Express your andwer to three significant figures and include the appropriate units.
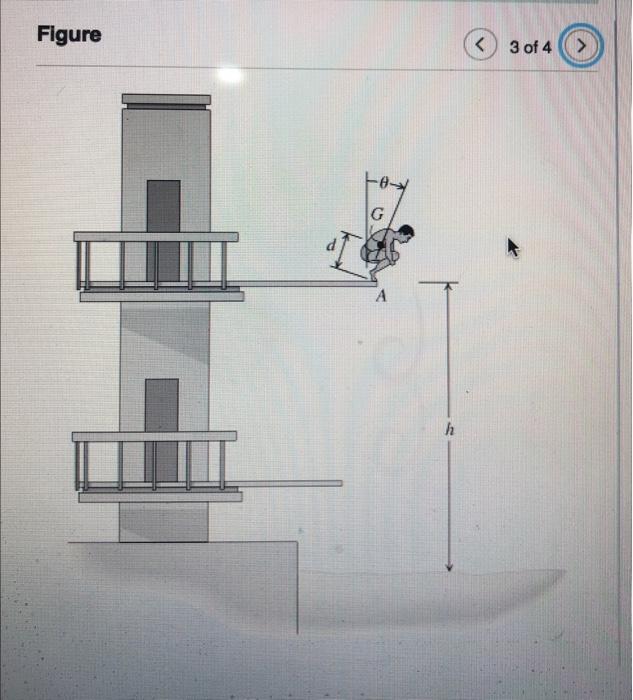
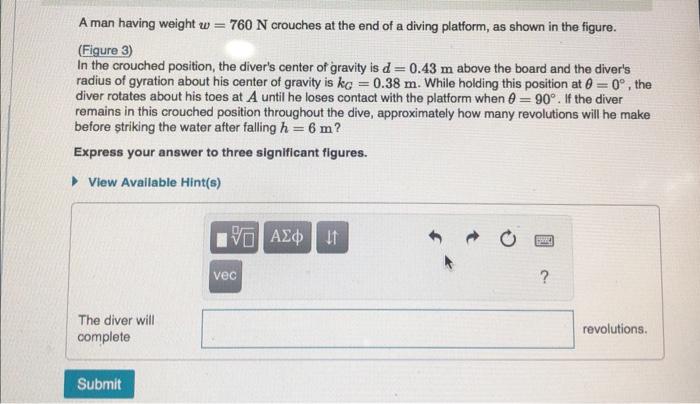
A man having weight crouches at the end of a diving platform, as shown in the figure. (Figure 3) In the crouched position, the diver's center of gravity is above the board and the diver's radius of gyration about his center of gravity is . While holding this position at , the diver rotates about his toes at until he loses contact with the platform when . If the diver remains in this crouched position throughout the dive, approximately how many revolutions will he make before striking the water after falling ? Express your answer to three significant figures.
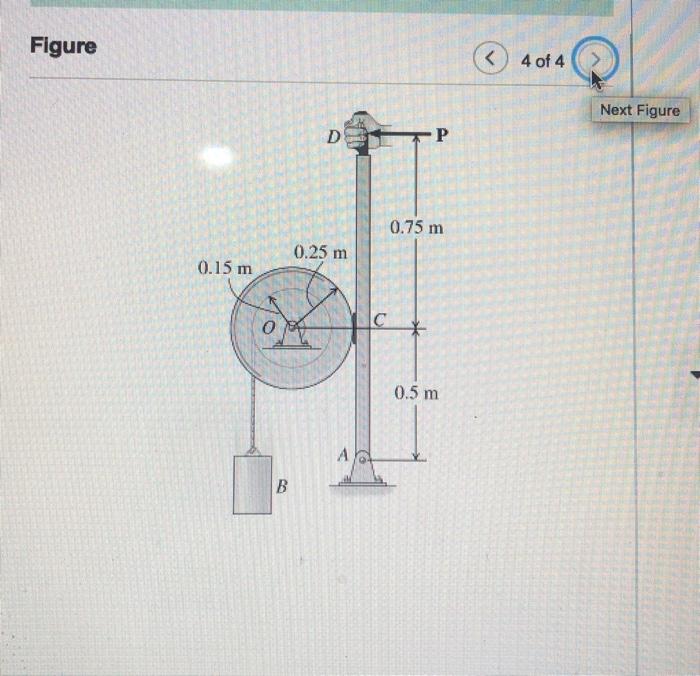
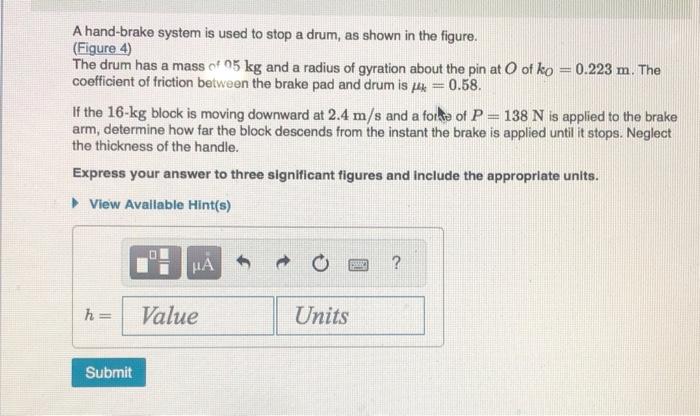
A hand-brake system is used to stop a drum, as shown in the figure. (Figure 4) The drum has a mass of and a radius of gyration about the pin at of . The coefficient of friction between the brake pad and drum is . If the 16 -kg block is moving downward at and a forhte of is applied to the brake arm, determine how far the block descends from the instant the brake is applied until it stops. Neglect the thickness of the handle. Express your answer to three significant figures and include the appropriate units.
Expert Answer
Solution-:Part A- Solution? Given datak=1,140 N/mm=15.2 kgx1=332 mm (stretched)x?=300 mm (released)V=0.220 m/sx=??Ti+Unet=TfGain in K.E.=Loss in