Home /
Expert Answers /
Advanced Math /
let-a-x-int-0-x-f-t-d-t-with-f-x-as-in-figure-alpha-x-has-a-local-min-pa522
(Solved): Let \( A(x)=\int_{0}^{x} f(t) d t \), with \( f(x) \) as in figure. \( \alpha(x) \) has a local min ...
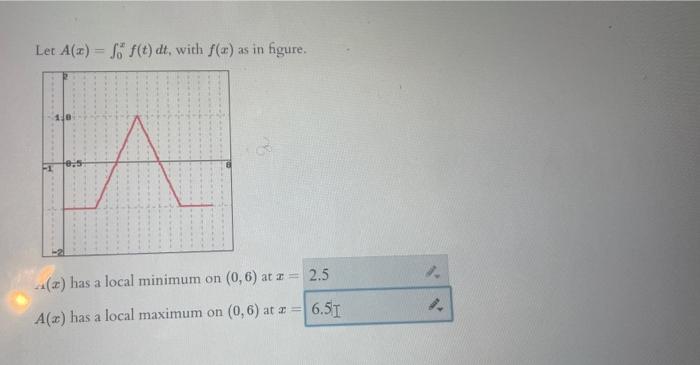
Let \( A(x)=\int_{0}^{x} f(t) d t \), with \( f(x) \) as in figure. \( \alpha(x) \) has a local minimum on \( (0,6) \) at \( x= \) \( A(x) \) has a local maximum on \( (0,6) \) at \( x= \)
Expert Answer
we have the fundamental theorem, therefore, f(x) = 0 at x=2.5, 4.5 hence, When the derivative crosses the x-axis, that means the function has a loc