Home /
Expert Answers /
Calculus /
let-mathrm-r-be-the-region-bounded-by-y-x-2-and-y-sqrt-8-x-find-the-volume-pa949
(Solved): Let \( \mathrm{R} \) be the region bounded by \( y=x^{2} \) and \( y=\sqrt{8 x} \). Find the volume ...
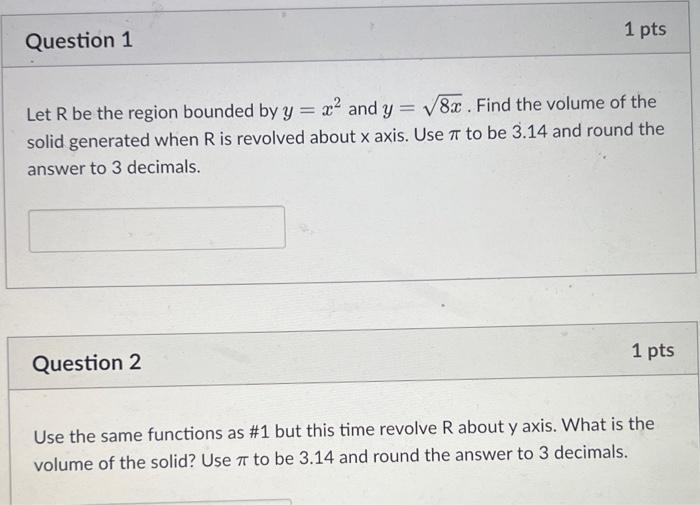
Let \( \mathrm{R} \) be the region bounded by \( y=x^{2} \) and \( y=\sqrt{8 x} \). Find the volume of the solid generated when \( R \) is revolved about \( x \) axis. Use \( \pi \) to be \( 3.14 \) and round the answer to 3 decimals. Question 2 \( 1 \mathrm{pts} \) Use the same functions as \#1 but this time revolve \( R \) about \( y \) axis. What is the volume of the solid? Use \( \pi \) to be \( 3.14 \) and round the answer to 3 decimals.
Expert Answer
The given curves are y=x2,y=8x If we calculate their intersection we found that the intersect at (0,0) and (2,4). So the region R bounded by above cur