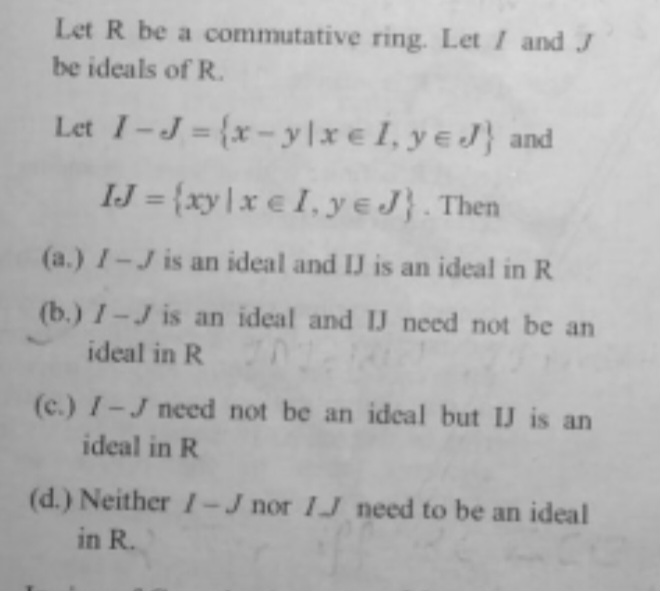(Solved): Let R be a commutative ring. Let I and J be ideals of R. Let I-J={x-y|xinI,yinJ} and IJ={xy|xinI,yi ...

Let R be a commutative ring. Let

and

be ideals of

. Let

and

. Then (a.)

is an ideal and

is an ideal in

(b.)

is an ideal and IJ need not be an ideal in R (c.)

need not be an ideal but IJ is an ideal in R (d.) Neither

nor

need to be an ideal in R .