(Solved): Let \( \theta \) be the angle between \( \mathbf{u} \) and \( v \). \[ \mathbf{u}=\left[\begin{arra ...

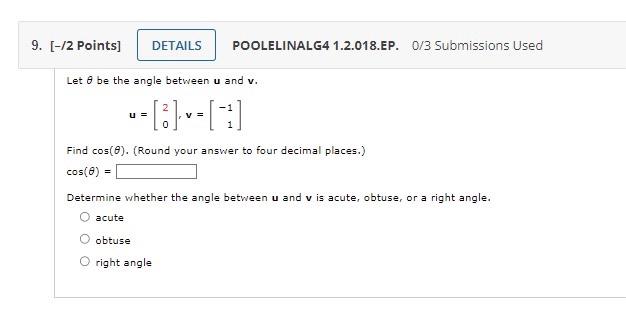
Let \( \theta \) be the angle between \( \mathbf{u} \) and \( v \). \[ \mathbf{u}=\left[\begin{array}{l} 2 \\ 0 \end{array}\right], \mathbf{v}=\left[\begin{array}{r} -1 \\ 1 \end{array}\right] \] Find \( \cos (\theta) \). (Round your answer to four decimal places.) \[ \cos (\theta)= \] Determine whether the angle between \( \mathbf{u} \) and \( v \) is acute, obtuse, or a right angle. 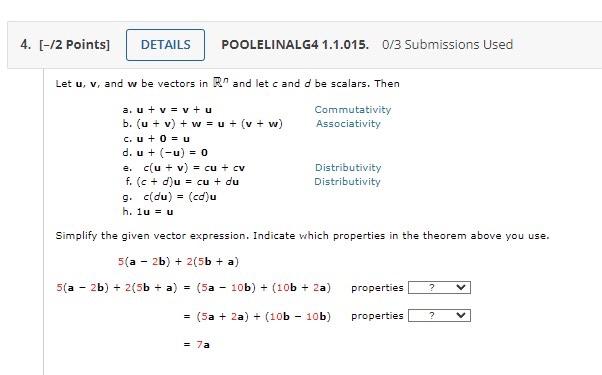acute obtuse right angle Let \( \mathbf{u}, \mathbf{v} \), and \( w \) be vectors in \( \mathbb{R}^{n} \) and let \( c \) and \( d \) be scalars. Then a. \( u+v=v+u \quad \) Commutativity b. \( (\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w}) \quad \) Associativity c. \( u+0=u \) d. \( \mathbf{u}+(-\mathbf{u})=0 \) e. \( c(\mathbf{u}+\mathbf{v})=c \mathbf{u}+c \mathbf{v} \quad \) Distributivity f. \( (c+d) \mathbf{u}=c \mathbf{u}+d \mathbf{u} \quad \) Distributivity g. \( c(d \mathbf{u})=(c d) \mathbf{u} \) h. \( 1 u=u \) Simplify the given vector expression. Indicate which properties in the theorem above you use. \[ \begin{array}{rlr} 5(\mathbf{a}-2 \mathbf{b})+ & 2(5 \mathbf{b}+\mathbf{a}) \\ 5(\mathbf{a}-2 \mathbf{b})+2(5 \mathbf{b}+\mathbf{a}) & =(5 \mathbf{a}-10 \mathbf{b})+(10 \mathbf{b}+2 \mathbf{a}) \quad \text { properties } \\ & =(5 \mathbf{a}+2 \mathbf{a})+(10 \mathbf{b}-10 \mathbf{b}) \quad \text { properties } \\ & =7 \mathbf{a} \end{array} \]