Home /
Expert Answers /
Calculus /
let-u-and-be-orthogonal-vectors-in-r-34-prove-that-proof-since-and-are-orthog-pa985
(Solved): Let u and be orthogonal vectors in R", prove that ||- ||||||+||||. Proof: Since and are orthog ...
Let u and be orthogonal vectors in R", prove that ||- ||²||||²+||||². Proof: Since and are orthogonal then ||ū – ī||² = A E. -7 0 from which it follows that, |=||||²+||||² A. (-+) - 2(-) B.||-||+|| C. (-)-(-) D. ||ū||² + |||||||| – ||v||||ū|| + || − 3||² F. (u1, u2, u3) (v1, v2, v3) = 0 Q.E.D.
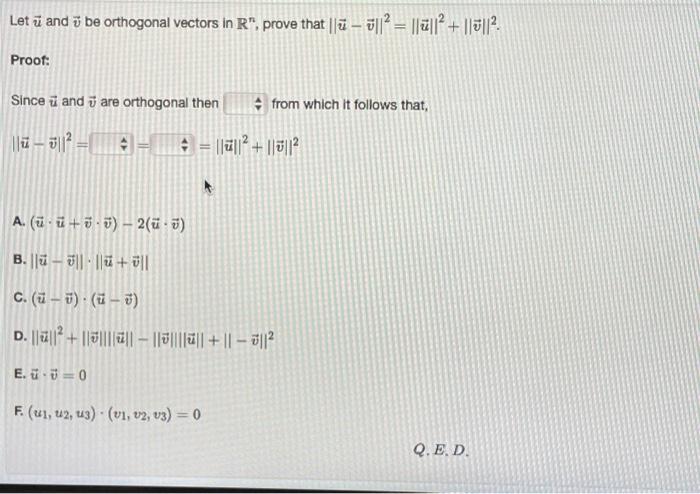
Let and be orthogonal vectors in , prove that . Proof: Since and are orthogonal then from which it follows that, A. B. C. D. E.
Expert Answer
By the definition of orthogonal vectors we have two vectors and are said to be orthogonal if Also the noram of a vector is defined by,