(Solved): Let U=(U1,U2,) represent an infinite sequence of coin tosses, with Ui=1 if the i th tos ...

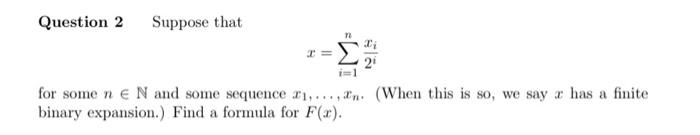
Let $U=\left(U_1,U_2,\dots \right)$ represent an infinite sequence of coin tosses, with $U_i=1$ if the $i$ th toss is heads and $U_i=0$ if it is tails. Suppose the coin tosses are independent, and that the probability of heads is $p\in (0,1)$ and the probability of tails is $q=1-p$. Given such a sequence we can define a real-valued random variable $X=f(U)$, taking values in the interval $[0,1]$, by $f(U)={\sum }_{i=1}^{\infty }\frac{U_i}{2^i}.$ We may think of $U$ as a binary expansion of $X$ (though in fact some $x\in [0,1]$ do not have a unique binary expansion, to wit, $0.1=0.01111\dots$.. Define the cumulative distribution function $F(x)=\mathbb{P}(X⩽x).$ For most values of $p$ the function $F$ is pathological, but it does have some interesting properties. Question 2 Suppose that $x={\sum }_{i=1}^n\frac{x_i}{2^i}$ for some $n\in \mathbb{N}$ and some sequence $x_1,\dots ,x_n$. (When this is so, we say $x$ has a finite binary expansion.) Find a formula for $F(x)$.