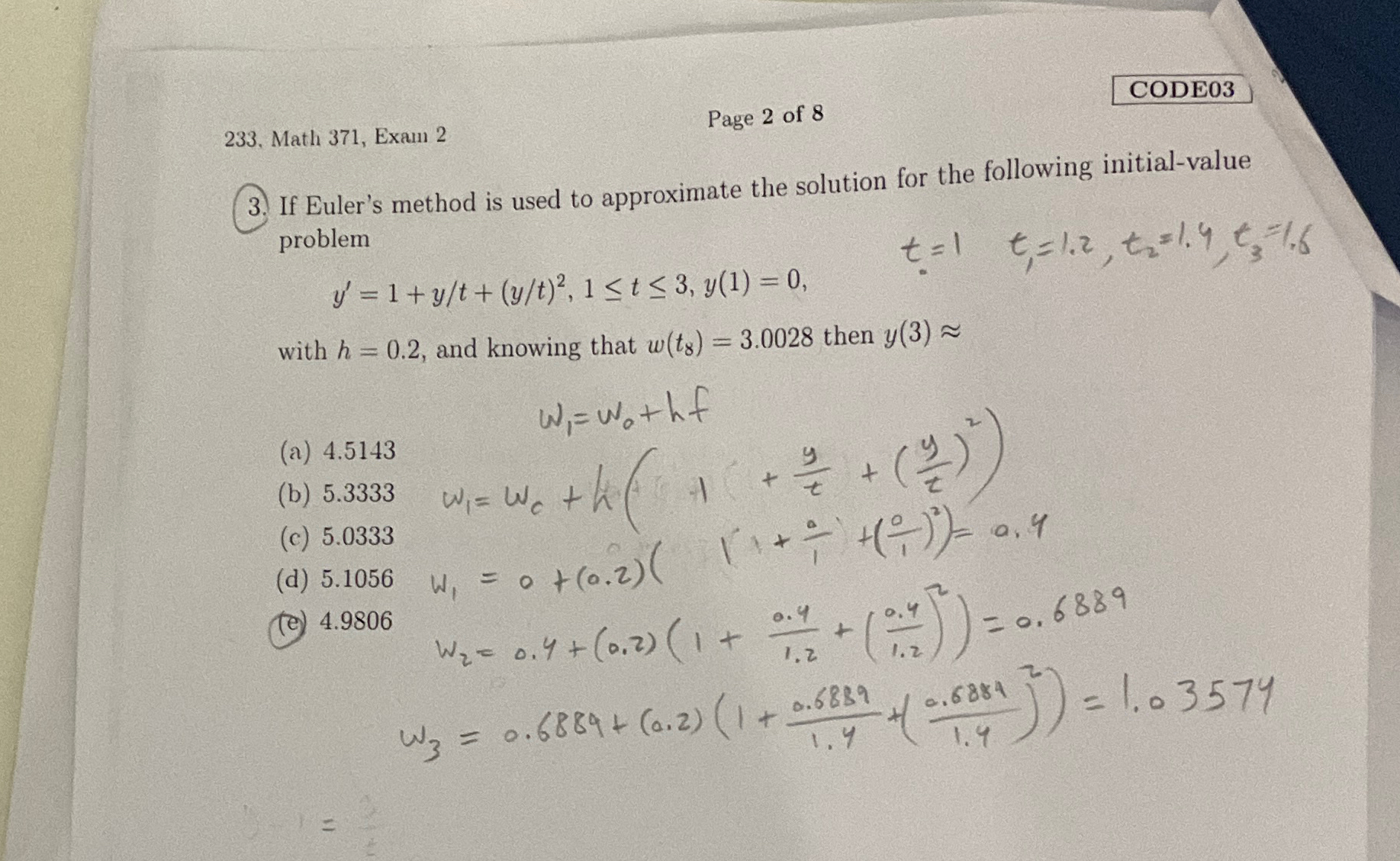Math 371, Exam 2 Page 2 of 8 CODE03 If Euler's method is used to approximate the solution for the following initial-value problem y^(')=1+(y)/(t)+((y)/(t))^(2),1

Question

Math 371, Exam 2 Page 2 of 8 CODE03 If Euler's method is used to approximate the solution for the following initial-value problem

y^(')=1+(y)/(t)+((y)/(t))^(2),1<=t<=3,y(1)=0,t=1,t=1.2,t_(2)=1.4,t_(3)=1.6

with

h=0.2

, and knowing that

w(t_(8))=3.0028

then

y(3)~~

(a) 4.5143

w_(1)=w_(0)+hf

(b) 5.3333 (c) 5.0333 (d) 5.1056 (e) 4.9806

w_(1)=w_(0)+hf
w_(1)=w_(0)+h(1+(y)/(t)+((y)/(t))^(2))
w_(1)=0+(0.2)(1+(0)/(1)+((0)/(1))^(2))=0.4

w_(2)=0.4+(0.2)(1+(0.4)/(1.2)+((0.4)/(1.2))^(2))=0.6889

Accepted Answer

Expert Answer to - Math 371, Exam 2 Page 2 of 8 CODE03 If Euler's method is used to approximate the solution for the fo

Answer

Solution for - Math 371, Exam 2 Page 2 of 8 CODE03 If Euler's method is used to approximate the solution for the fo

Answer

This an additional answer to - Math 371, Exam 2 Page 2 of 8 CODE03 If Euler's method is used to approximate the solution for the fo

(Solved): Math 371, Exam 2 Page 2 of 8 CODE03 If Euler's method is used to approximate the solution for the fo ...