(Solved): Matrix A is factored in the form PDP^(-1). Use the Diagonalization Theorem to find the eigenvalues o ...

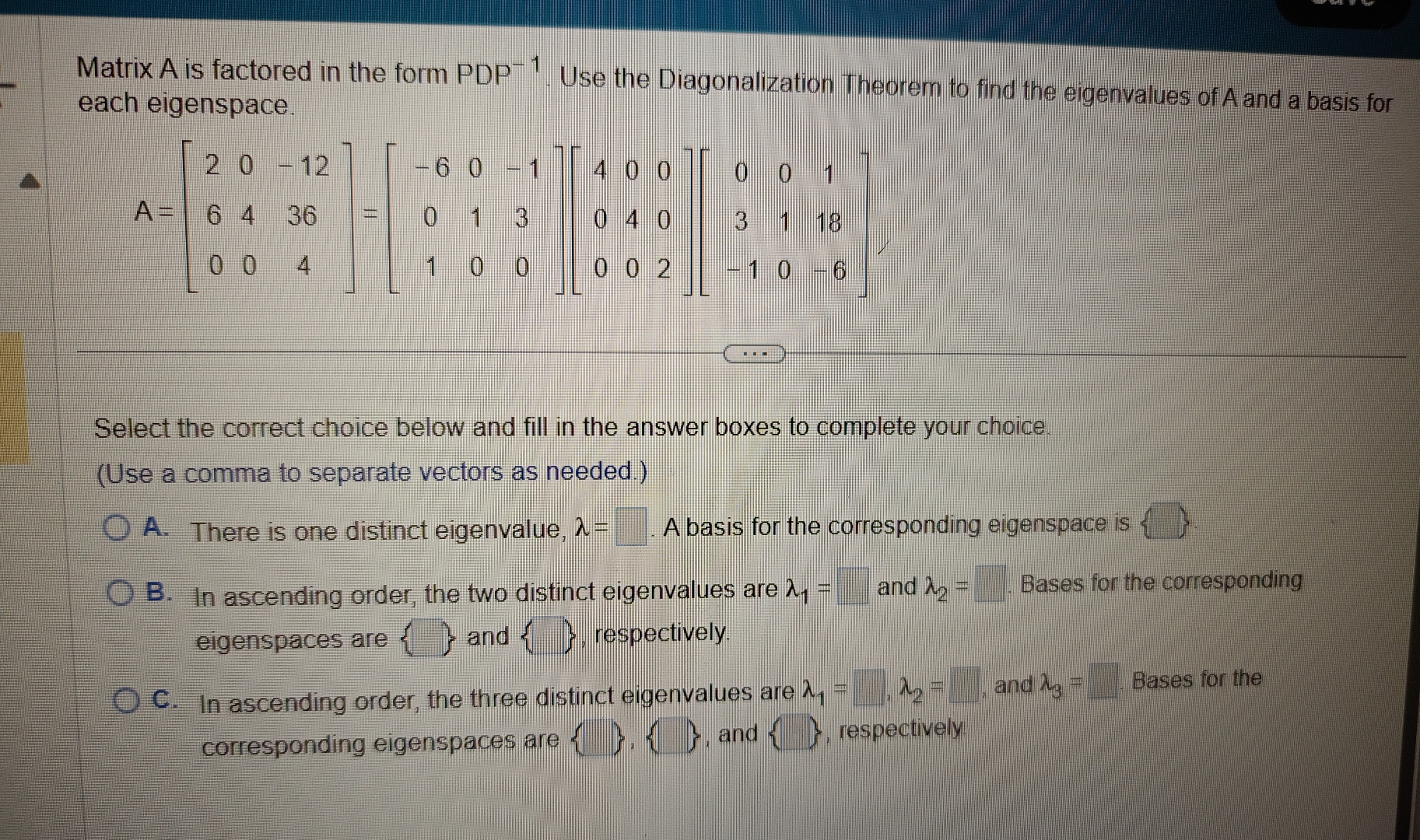
Matrix A is factored in the form

. Use the Diagonalization Theorem to find the eigenvalues of

and a basis for each eigenspace.

Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) A. There is one distinct eigenvalue,

A basis for the corresponding eigenspace is

B. In ascending order, the two distinct eigenvalues are

and

Bases for the corresponding eigenspaces are

and

respectively. C. In ascending order, the three distinct eigenvalues are

and

Bases for the corresponding eigenspaces are {

, and

respectively