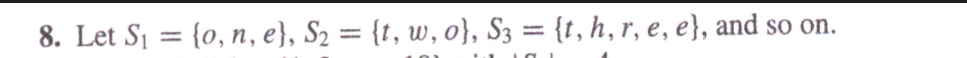(Solved):   8. Let \( S_{1}=\{o, n, e\}, S_{2}=\{t, w, o\}, S_{3}=\{t, h, r, e, e\} \), and so on. ...

 

8. Let \( S_{1}=\{o, n, e\}, S_{2}=\{t, w, o\}, S_{3}=\{t, h, r, e, e\} \), and so on. 3. Let \( S_{1}, S_{2}, S_{3} \), etc. be defined as in Problem 8 in Section 1.1. (a). Find all \( k \in\{1,2, \ldots, 20\} \) with \( \left|S_{k}\right| \leq 5 \). (b). Find three distinct indices \( h, i, j \in \mathbb{N} \) such that \( S_{h}=S_{i}=S_{j} \). (c). Find the smallest value of \( k \in \mathbb{N} \) such that \( y \in S_{k} \). (d). Let \( \mathcal{S}=\left\{S_{k}\right\}_{k=1}^{70} \). Determine whether the following are true or false. (i). \( S_{35}=\{v, e, r, i, f, y\} \) (ii). \( \left|S_{35}\right|>\left|S_{53}\right| \) (iii). \( \mathcal{P}\left(S_{10}\right) \subseteq \mathcal{P}\left(S_{13}\right) \) (iv). \( |A|>2 \) for all \( A \in \mathcal{S} \) (v). \( |\mathcal{S}|=70 \)