Home /
Expert Answers /
Advanced Math /
nbsp-abstract-algebra-please-explain-and-show-all-steps-let-a-and-b-be-elements-o-pa695
(Solved): Abstract Algebra Please explain and show all steps. Let \( a \) and \( b \) be elements o ...
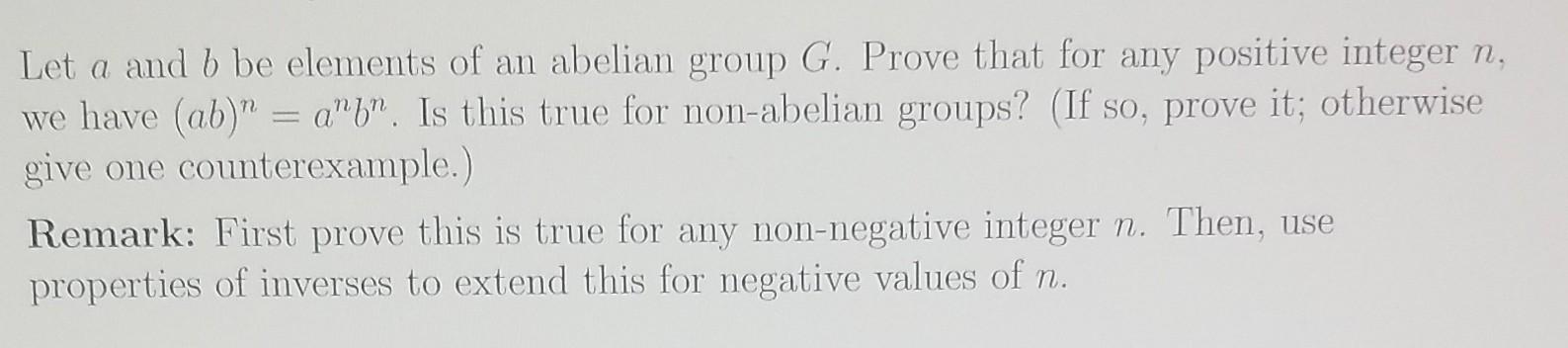
Abstract Algebra
Please explain and show all steps.
Let \( a \) and \( b \) be elements of an abelian group \( G \). Prove that for any positive integer \( n \), we have \( (a b)^{n}=a^{n} b^{n} \). Is this true for non-abelian groups? (If so, prove it; otherwise give one counterexample.) Remark: First prove this is true for any non-negative integer \( n \). Then, use properties of inverses to extend this for negative values of \( n \).