(Solved):       due in 30 min Which of the following is true about a confidence interva ...

 

 

 

due in 30 min

Which of the following is true about a confidence interval for the population mean? 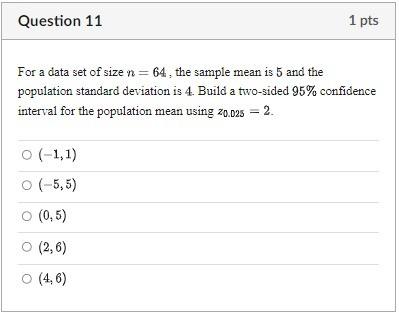It is an interval determined by a lower and upper bound, such that when seen as random bounds, the probability of the population mean being in the interval is \( (1-\alpha) \) It always contains the population mean It is the best point estimate of the population mean It is a single number: the true value of the population mean It consists of as many numbers as possible For a data set of size \( n=64 \), the sample mean is 5 and the population standard deviation is 4 . Build a two-sided \( 95 \% \) confidence interval for the population mean using \( z_{0.025}=2 \). 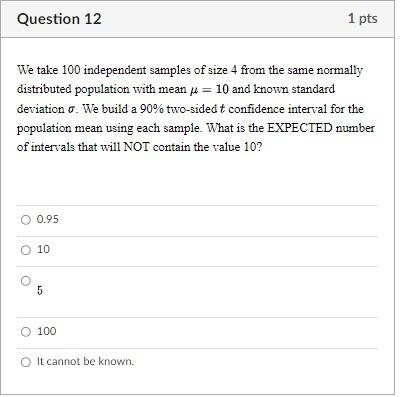\( (-1,1) \) \( (-5,5) \) \( (0,5) \) \( (2,6) \) \( (4,6) \) We take 100 independent samples of size 4 from the same normally distributed population with mean \( \mu=10 \) and known standard deviation \( \sigma \). We build a \( 90 \% \) two-sided \( t \) confidence interval for the population mean using each sample. What is the EXPECTED number of intervals that will NOT contain the value 10 ? \( 0.95 \) 10 5 100 It cannot be known.