Home /
Expert Answers /
Calculus /
nbsp-nbsp-nbsp-nbsp-solve-them-please-find-the-derivative-of-y-with-respect-pa524
(Solved): Solve them please Find the derivative of \( y \) with respect ...
![Find the derivative of \( y \) with respect to \( x \).
\[
y=e\left(4 \sqrt{x}+x^{6}\right)
\]
A. \( \left(\frac{2}{\sqrt{x}}](https://media.cheggcdn.com/study/d34/d342385e-f8ef-4385-b406-aa4575e6f57e/image.jpg)
![Find the derivative of \( y \) with respect to \( t \).
\[
y=e^{\sin t}\left(\ln t^{4}+6\right)
\]
A. \( e^{\sin t}\left(\ln](https://media.cheggcdn.com/study/2ee/2ee0da9e-0ace-4460-b67e-a33bd62826df/image.jpg)

Solve them please
Find the derivative of \( y \) with respect to \( x \). \[ y=e\left(4 \sqrt{x}+x^{6}\right) \] A. \( \left(\frac{2}{\sqrt{x}}+6 x^{5}\right) e^{\left(4 \sqrt{x}+x^{6}\right)} \) B. \( e^{\left(2 \sqrt{x}+6 x^{5}\right)} \) C. \( \left.4 \sqrt{x}+6 x^{5}\right) e\left(4 \sqrt{x}+x^{6}\right) \) D. \( \left(4 \sqrt{x}+6 x^{5}\right) \ln \left(4 \sqrt{x}+x^{6}\right) \)
Find the derivative of \( y \) with respect to \( t \). \[ y=e^{\sin t}\left(\ln t^{4}+6\right) \] A. \( e^{\sin t}\left(\ln t^{4}+6+\frac{4}{t}\right) \) B. \( e^{\sin t}\left((\cos t)\left(\ln t^{4}+6\right)+\frac{4}{t}\right) \) C. \( e^{\cos t}(\cos t)\left(\ln t^{4}+6\right)+\frac{4 e^{\sin t}}{t} \) D. \( \frac{4 e^{\sin t} \cos t}{t} \)
\( \frac{d y}{d x} \) \( 8 x y=e^{x+y} \) A. \( \frac{2 x y e^{x+y}}{x+y} \) B. \( \frac{e^{x+y}}{e^{8 x}} \) C. \( \frac{y}{x} \) D. \( \frac{x y e^{x+y}-y}{x-x y e^{x+y}} \)
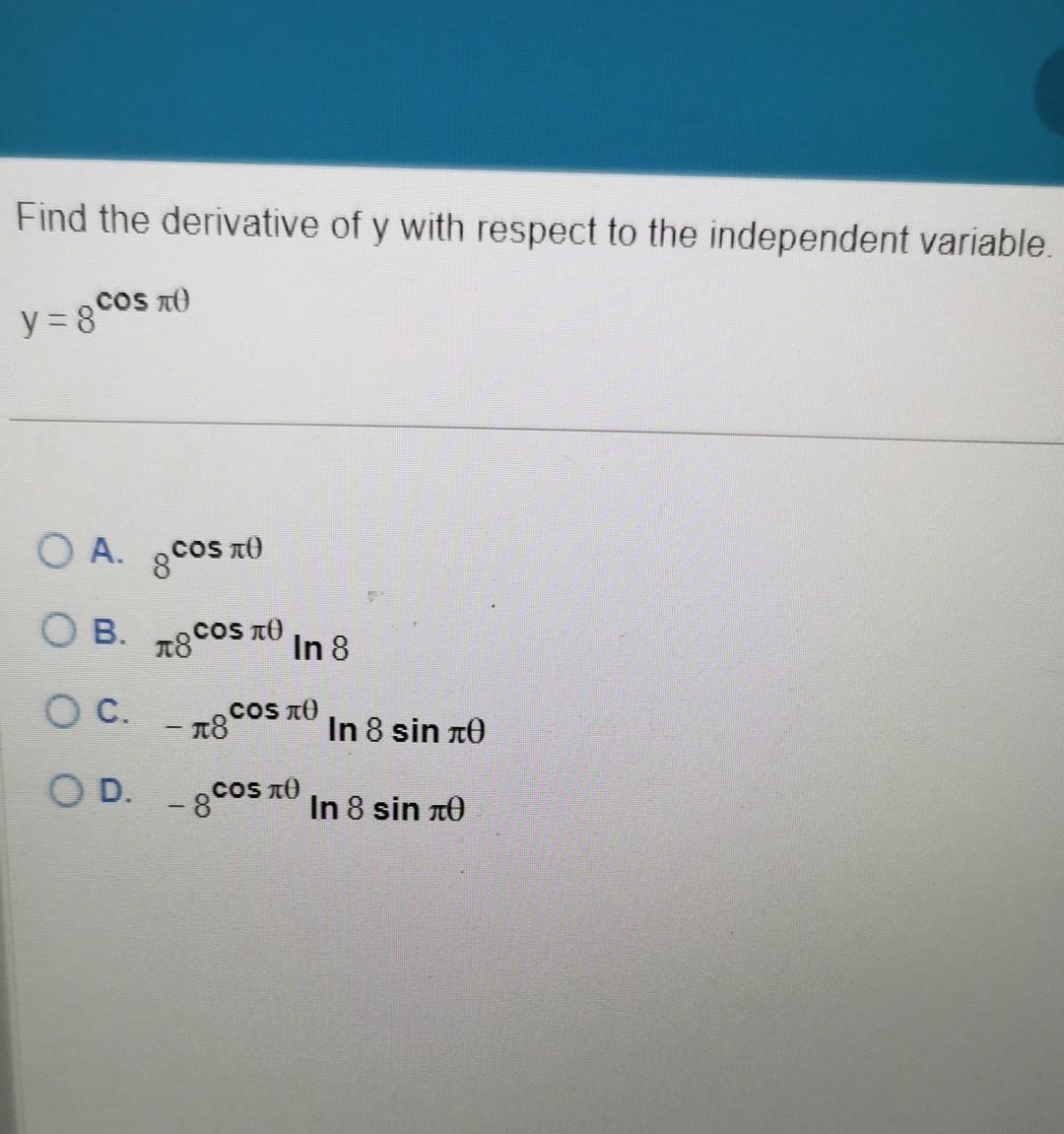
Find the derivative of \( y \) with respect to the independent variable. \( y=8^{\cos \pi \theta} \) A. \( 8^{\cos \pi \theta} \) B. \( \pi 8^{\cos \pi \theta} \ln 8 \) C. \( -\pi 8^{\cos \pi \theta} \ln 8 \sin \pi \theta \) D. \( -8^{\cos \pi \theta} \ln 8 \sin \pi \theta \)
Expert Answer
Given y=e(4x+x6) Differentiating w.r.t x dydx=ddxe(4x+x6)=e(4x+x6)×ddx(4x+x6)=e(4x+x6)×(4ddx(x)12+ddxx6) As we know that ddxxn=nxn?1 and chain rule dy