(Solved):     The type of the DeModulation system where the output noise has only the inphas ...

 

 

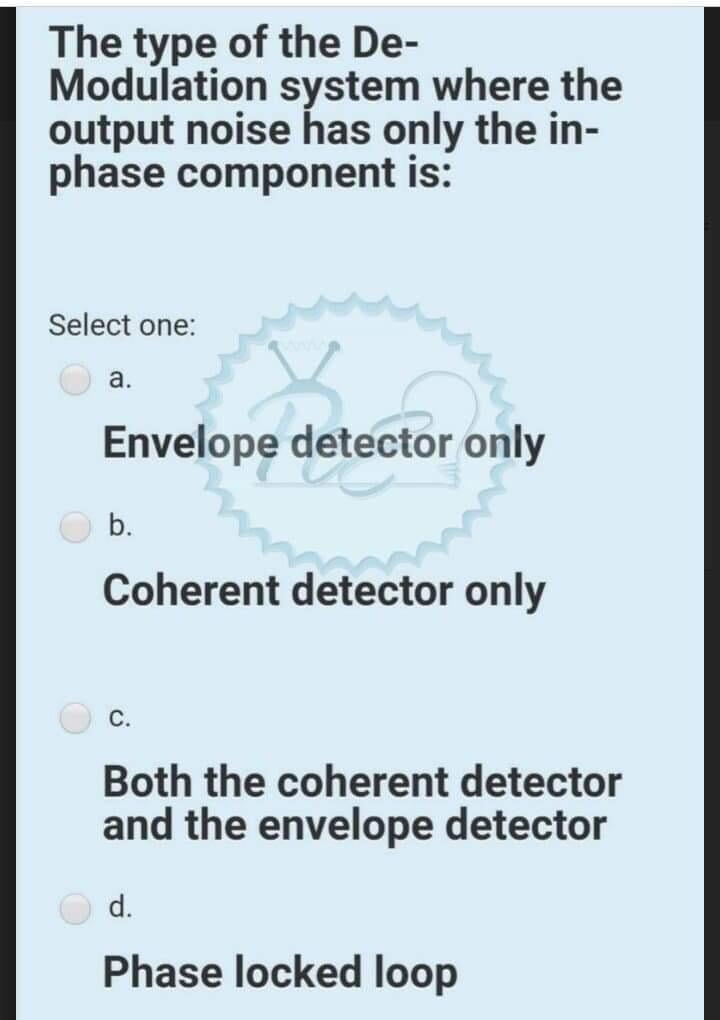
The type of the DeModulation system where the output noise has only the inphase component is: Select one: a. Envelope detector only b. Coherent detector only c. Both the coherent detector and the envelope detector d. Phase locked loop For an AWGN, The power spectral density is \( S_{w}(f)=\frac{N_{0}}{2} \), the autocorrelation function given as \( R_{w}(\tau) \) would be: Select one: a. \( R_{w}(\tau)=F . T,{ }^{-1} S_{w}(f) \) \( R_{w}(\tau)=\frac{N_{0}}{2} \frac{d}{d \tau} S_{w}(f) \) \( R_{w}(\tau)=\frac{N_{0}}{2} \exp ^{S_{w}(f)} \) d. \[ R_{w}(\tau)=\int \frac{N_{0}}{2} S_{w}(f) d f \] For an AWGN, the autocorrelation function given as \( R_{w}(\tau)=\frac{N_{0}}{2} \delta(\tau) \). The power spectral density \( S_{w}(f) \) of the \( \mathrm{AWGN} \) is: \[ \begin{array}{r} S_{w}(f)=\text { F.T.of } R_{w}(\tau) \\ S_{w}(f)=\frac{N_{0}}{2} \int R_{w}(\tau) d \tau \\ S_{w}(f)=\frac{N_{0}}{2} \exp ^{R_{w}(\tau)} \\ S_{w}(f)=\frac{N_{0}}{2} \frac{d}{d \tau} R_{w}(\tau) \end{array} \]