(Solved):   Q12   Q13   Q14   Q15 please answer all 4 questions Find the valu ...

 
Q12

 
Q13

 
Q14

 
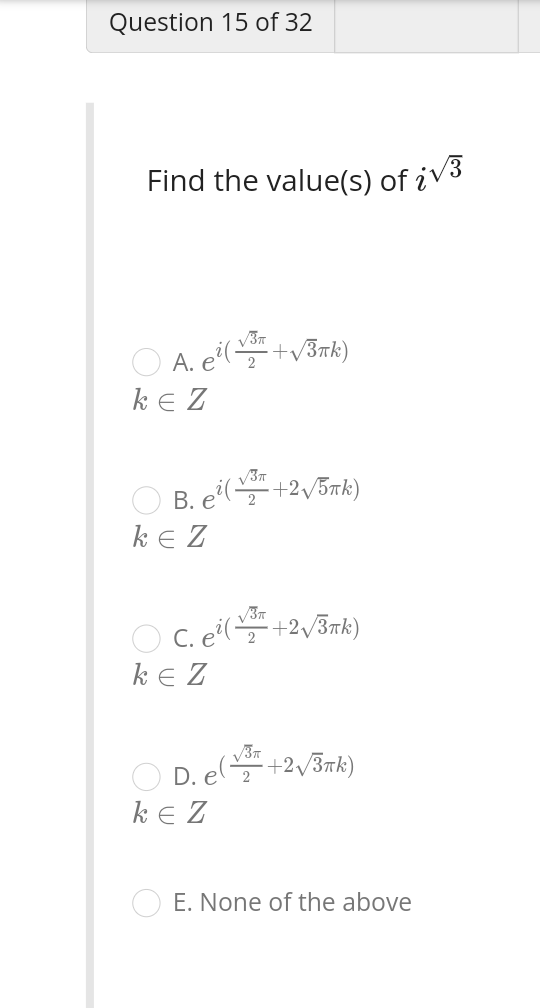
Q15
please answer all 4 questions

Find the value(s) of \( \log \left((1-i)^{4}\right) \) A. \( 2 \ln 2+i \pi(1-8 k) \) \( k \in Z \) B. \( 2 \ln 2-i \pi(1+8 k) \) \( k \in Z \) C. \( 2 i \ln 2+i \pi(1+8 k) \) \( k \in Z \) D. \( \ln 2+i \pi(1+8 k) \) ,\( k \in Z \) E. None of the above Use complex logarithms to reexpress \( i^{i} \) A. \( e^{-\frac{\pi}{2}-2 \pi n} \) \( , n=0,1,2,3 \ldots \ldots \) B. \( e^{-\frac{\pi}{2}-2 \pi n i} \) \( \mathrm{n}=0,1,2,3 \ldots \ldots \) C. \( e^{\frac{\pi}{2}-2 \pi n} \) \( \mathrm{n}=0,1,2,3 \ldots \ldots \) D. \( e^{-\frac{\pi}{2}+2 \pi n} \) \( , \mathrm{n}=0,1,2,3 \ldots \ldots \) E. None of the above Use complex logarithms to reexpress \( 2^{i} \) A. \( e^{2 \pi n-\ln 2} \) \( n=0,1,2,3 \ldots \ldots \) B. \( e^{2 i \pi n-\ln 2} \) \( n=0,1,2,3 \ldots \ldots \) C. \( e^{-2 \pi n+i \ln 2} \) \( n=0,1,2,3 \ldots \ldots \) D. \( e^{2} e^{2 \pi n-\ln 2} \) \( \mathrm{n}=0,1,2,3 \ldots \ldots \) E. None of the above Find the value(s) of \( i^{\sqrt{3}} \) \[ \begin{array}{l} \text { A. } e^{i\left(\frac{\sqrt{3} \pi}{2}+\sqrt{3} \pi k\right)} \\ k \in Z \\ \text { B. } e^{i\left(\frac{\sqrt{3} \pi}{2}+2 \sqrt{5} \pi k\right)} \\ k \in Z \\ \quad \text { C. } e^{i\left(\frac{\sqrt{3} \pi}{2}+2 \sqrt{3} \pi k\right)} \\ k \in Z \\ \quad \text { D. } e^{\left(\frac{\sqrt{3} \pi}{2}+2 \sqrt{3} \pi k\right)} \\ k \in Z \end{array} \] E. None of the above