(Solved):   Wrap a string around a pulley with a radius R = 0.20 m and a mass M = 2.0 kg that can ro ...

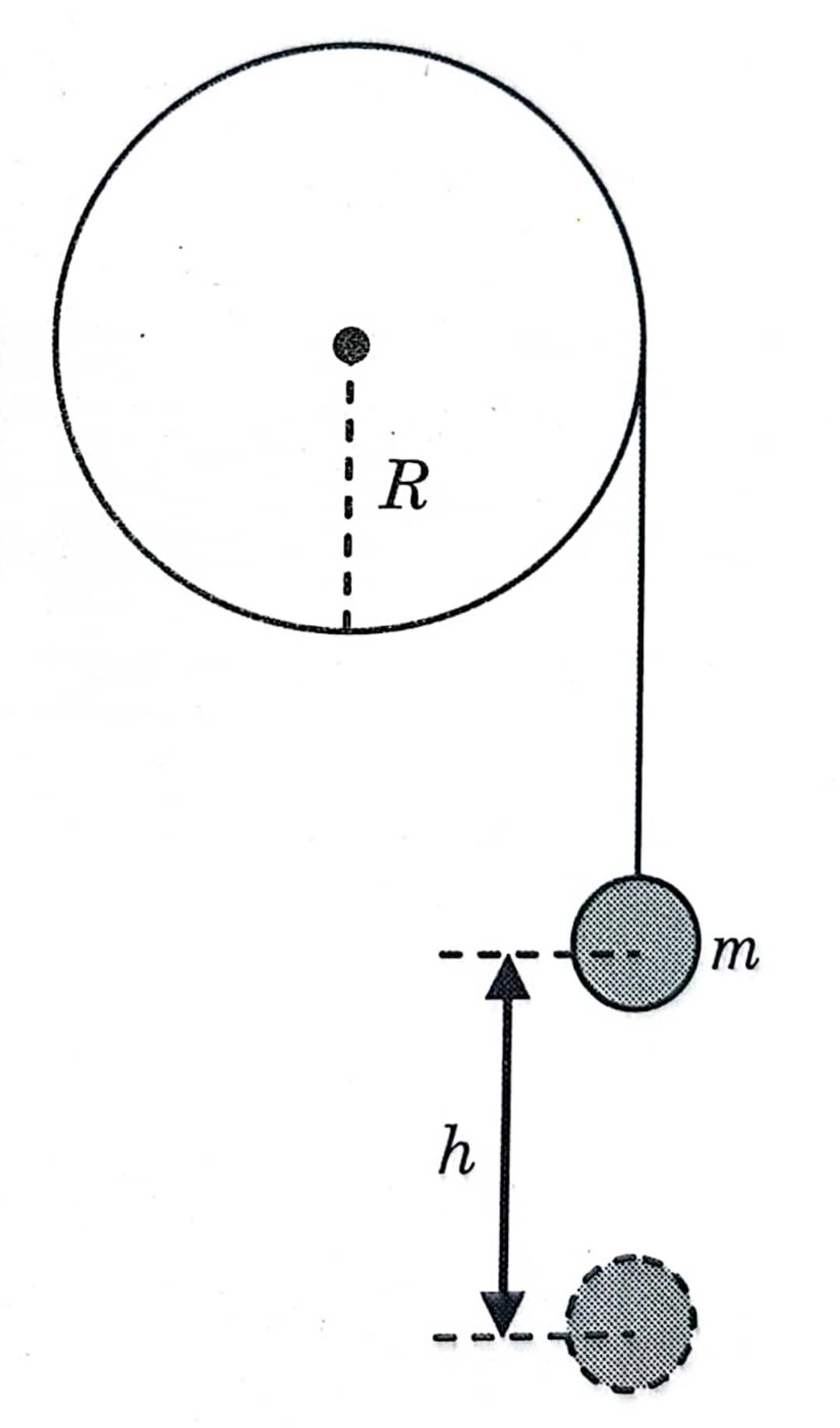
Wrap a string around a pulley with a radius R = 0.20 m and a mass M = 2.0 kg that can rotate freely around a friction-free shaft, and attach a weight with a mass m = 1.0 kg under the string as shown in the figure and release it.
Answer the following questions.  However, the moment of inertia of the pulley is I = 1 / 2MR ^ 2. 
(1) After releasing your hand, write the formula for mechanical energy conservation, where v is the speed of the weight when the weight falls by h, ? is the angular velocity of the pulley, and I is the moment of inertia of the pulley.
Answer:0=1/2I?^2+1/2mv^2-mgh
(2) Find the speed v of the weight when the weight falls by h = 0.50m.  Answer: v=?4mgh/M+m2=2.2 m/s
(3) Find the acceleration a of the weight. Answer: a=2mg/M+2m=4.9 m/s^2
(4) Find the angular velocity ? of the pulley when the weight falls by h = 0.50m.  Answer: ?=?4mgh/(M+2m)R^2=11 rad/s
(5) Find the angular acceleration ? of the pulley. Answer: ?=2mg/(M+2m)R=25 rad/s^2
how to solve the problem to get the same answers?