(Solved): PART \( 1 . \) Find the siope of the secant lne containing the points \( (a, f(a)) \) and \( \left( ...

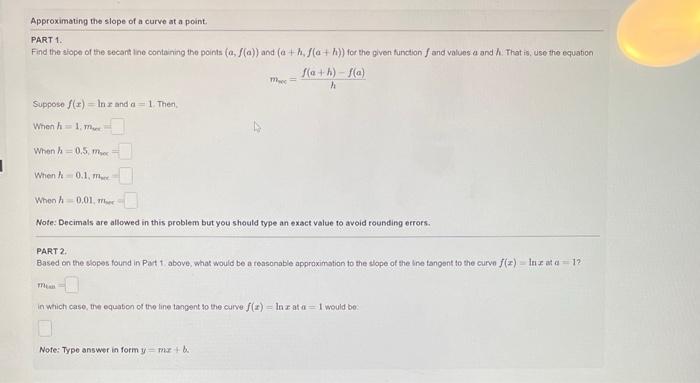
PART \( 1 . \) Find the siope of the secant lne containing the points \( (a, f(a)) \) and \( \left(a+h_{4} f(a+h)\right) \) for the given function \( f \) and values \( a \) and \( h \). That is, use the equation \[ m_{w<}=\frac{f(\alpha+h)-f(a)}{h} \] Supposo \( f(x)=\ln x \) and \( a=1 \). Then, When \( h=1 \), Muse \( ^{2}= \) When \( h=0,5, m_{n}= \) When \( h=0.1, m_{\text {sere }} \) When \( h=0,01 \), mose Note: Decimais are allowed in this problem but you should type an exact value to avoid rounding errors. PART? Based on the slopes found in Part t above, what would be a teasonable approximation to the slope of the ine tanpent to the curve \( f(x) \) - la \( I \) at a \( =1 \) ? mean = in which case, the equaton of the line tangent to the curve \( f(x)=\ln x \) at \( a=1 \) would be: Note: Type answer in form \( y=m x+b \) i