(Solved): Part A - Calculating the output voltage of a summing op amp circuit For the circuit shown(Figure 1) ...

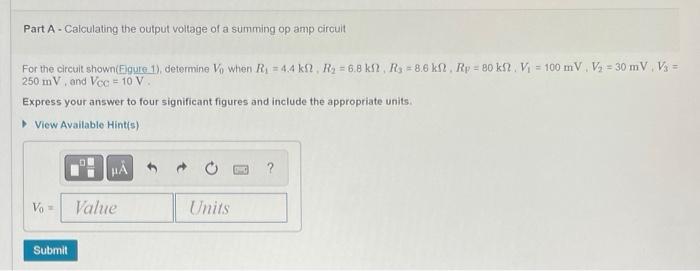
Part A - Calculating the output voltage of a summing op amp circuit For the circuit shown(Figure 1), determine \( V_{0} \) when \( R_{1}=4.4 \mathrm{k} \Omega, R_{2}=6.8 \mathrm{k \Omega} \Omega, R_{3}=8.6 \mathrm{k} \Omega, R_{p}=80 \mathrm{k} \Omega, V_{1}=100 \mathrm{mV}, V_{2}=30 \mathrm{mV}, V_{3}= \) \( 250 \mathrm{mV} \), and \( V_{\mathrm{CC}}=10 \mathrm{~V} \) Express your answer to four significant figures and include the appropriate units. 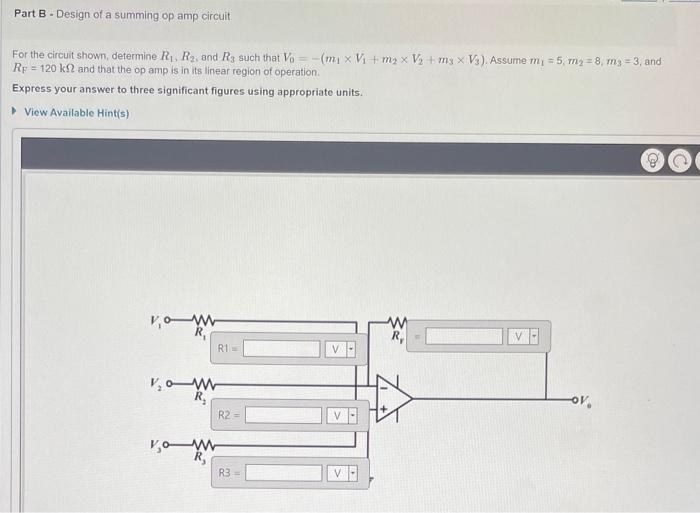1 of 2 For the circuit shown, determine \( R_{1}, R_{2} \), and \( R_{3} \) such that \( V_{0}=-\left(m_{1} \times V_{1}+m_{2} \times V_{2}+m_{3} \times V_{3}\right) \). Assume \( m_{1}=5, m_{2}=8, m_{3}=3 \), and \( R_{\mathrm{F}}=120 \mathrm{k} \Omega \) and that the op amp is in its linear region of operation. Express your answer to three significant figures using appropriate units. 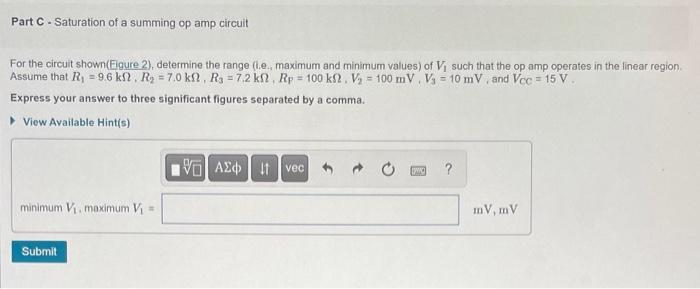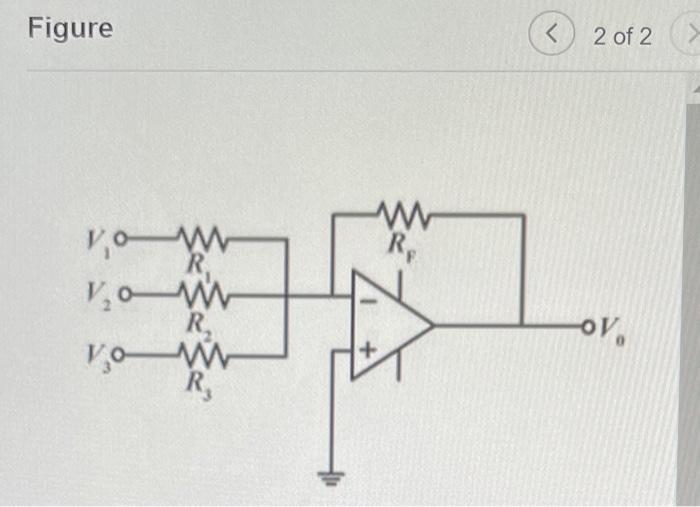View Available Hint(s) Part C - Saturation of a summing op amp circuit For the circuit shown(Eigure 2), determine the range (lie., maximum and minimum values) of \( V_{1} \) such that the op amp operates in the linear region. Assume that \( R_{1}=9.6 \mathrm{k} \Omega, R_{2}=7.0 \mathrm{k} \Omega, R_{3}=7.2 \mathrm{k} \Omega, R_{\mathrm{F}}=100 \mathrm{k} \Omega, V_{2}=100 \mathrm{mV}, V_{3}=10 \mathrm{mV} \), and \( V_{\mathrm{CC}}=15 \mathrm{~V} \). Express your answer to three significant figures separated by a comma. Figure 2 of 2