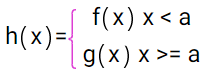(Solved): Part A: Make a piecewise function h(x) (format in the picture) that is not differentiable but is con ...

Part A: Make a piecewise function h(x) (format in the picture) that is not differentiable but is continuous at x = a. Let f(x) = 1/(x^3 + 2x). Create a g(x) different from f(x) and select the 'a' value. Type both your functions into a graphing software (https://www.desmos.com/calculator) and insert them below. Provide an explanation to explain why part A's piecewise function is not is not differentiable at x = a despite the function being continuous at x = a ('a' is chosen value).
Part B: Repeat part A with the same f(x) = 1/(x^3 + 2x) and the same chosen 'a' value, and choose a new or keep the same g(x) function, and create a piecewise function h(x) that IS differentiable at x = a. Then insert the graph piecewise function, and provide an algebraic solution to prove the piecewise function is differentiable at x = a. First prove continuity and then differentiability. Use proper limit notation.