Home /
Expert Answers /
Calculus /
part-f-says-34-give-the-macimum-value-of-p-as-well-as-the-two-numbers-x-and-y-for-which-x-2y-is-that-pa630
(Solved): part f says "give the macimum value of P, as well as the two numbers x and y for which x^2y is that ...
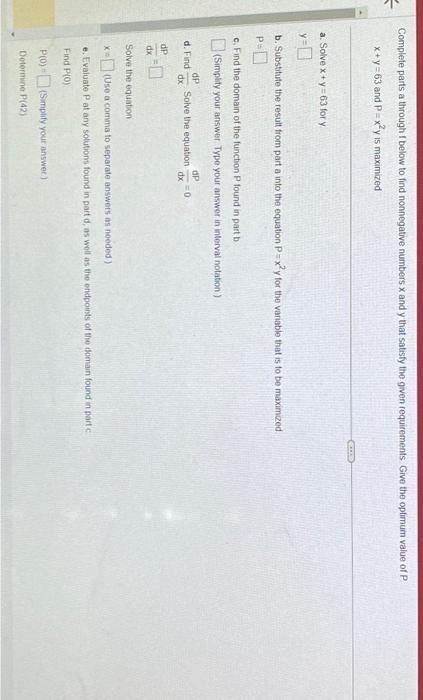
part f says "give the macimum value of P, as well as the two numbers x and y for which x^2y is that value".
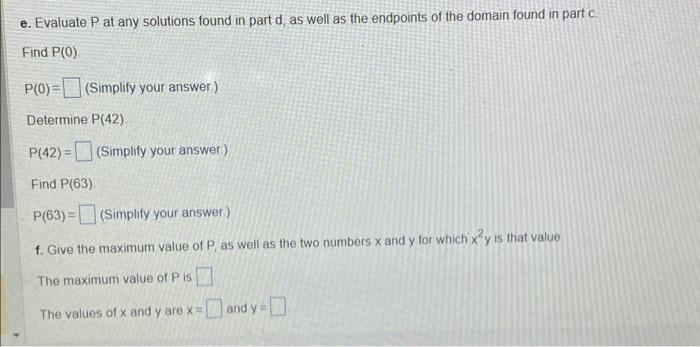
Complefe parts a through I below to find nonnegative numbers \( x \) and \( y \) that satisfy the given requirements Give the optimum value of \( P \). \( x+y=63 \) and \( P=x^{2} y \) is maximized a. Solve \( x+y=63 \) for \( y \) \[ y= \] b. Substitute the result from part a into the equation \( P=x^{2} y \) for the variable that is to be maximzed \( P= \) c. Find the domain of the functoon \( P \) tound in part \( b \) (Simplity your answer Type your answer in interval notation) d. Find \( \frac{d P}{d x} \) Solve the equation \( \frac{d P}{d x}=0 \) \[ \frac{d P}{d x}= \] Solve the equation \( \mathrm{x}= \) (Use a comma to separate answets is noeded) e. Evaluate \( \mathrm{P} \) at any solutions found in part \( \mathrm{d} \), as weil as the endpoints of the domain found in part \( \mathrm{C} \) Find \( \mathrm{P}(0) \) \( P(0) \) - (Simplify your answee) Dotermine P(42)
e. Evaluate \( P \) at any solutions found in part d, as well as the endpoints of the domain found in part \( c \). Find \( \mathrm{P}(0) \) \[ P(0)= \] (Simplify your answer.) Determine \( P(42) \) \[ P(42)= \] (Simplify your answer) Find \( \mathrm{P}(63) \). \[ P(63)=\text { (Simplify your answer) } \] f. Give the maximum value of \( P \), as well as the two numbers \( x \) and \( y \) for which \( x^{2} y \) is that value The maximum value of \( P \) is The values of \( x \) and \( y \) are \( x=\quad \) and \( y= \)
Expert Answer
(a) we have x+y=63?y=63?x (b) given P=x2y putting the value of y obtained from (a), we get P=x2(63?x)=63x2?x3