(Solved): Please answer the following questions SHOWING ALL WORK ACCORDINGLY ON ALL PARTS AND SECTIONS. Thank ...

Please answer the following questions SHOWING ALL WORK ACCORDINGLY ON ALL PARTS AND SECTIONS. Thank you!

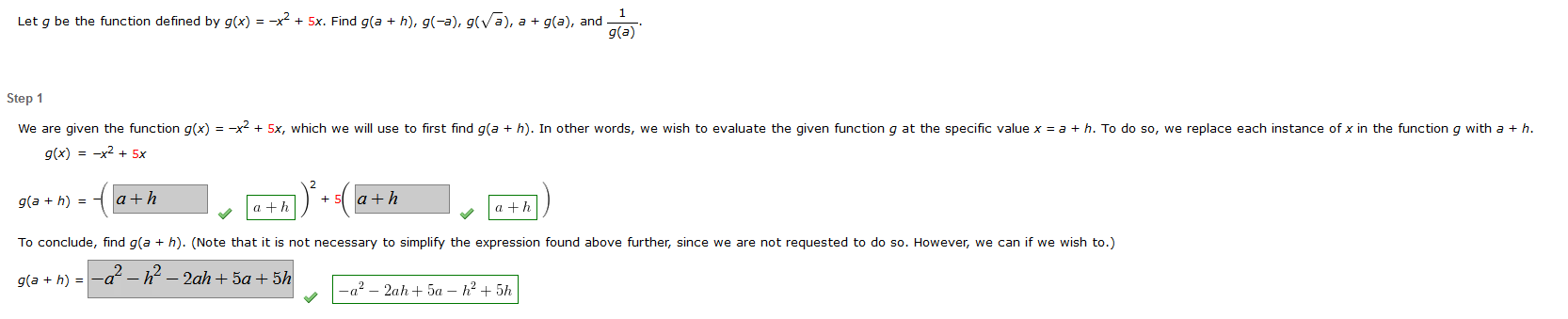
Let g be the function defined by g(x) = -x² + 5x. Find g(a + h), g(?a), g(??), a + g(a), and 1 g(a) Step 1 We are given the function g(x) = -x² + 5x, which we will use to first find g(a + h). In other words, we wish to evaluate the given function g at the specific value x = a + h. To do so, we replace each instance of x in the function g with a + h. g(x) = -x² + 5x g(a + h) = a+h 7) ²³ + 5 ( a + h a+h a+h To conclude, find g(a + h). (Note that it is not necessary to simplify the expression found above further, since we are not requested to do so. However, we can if we wish to.) g(a + h) = ? a² - h² - 2ah+5a +5h -a² - 2ah+5a - h² + 5h ? 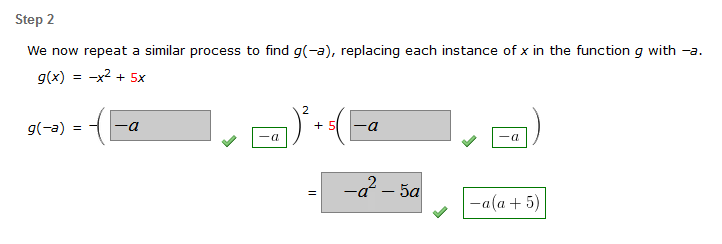Step 2 We now repeat a similar process to find g(-a), replacing each instance of x in the function g with -a. g(x) = -x² + 5x 2 g(-a) = -a 7) ². a -a -a² - 5a -a(a + 5) -a + 5 || To find g(?a), replace each instance of x in the function g with ?a. g(x) = -x² + 5x 2 ])² + + 5(?a) 9(??) = ([ || Find and simplify f(a+h)-f(a) for the following function. f(x) = 5x²15x + 8 Step 1 To find f(a + h) ? f(a) given f(x) = 5x² - 15x + 8, it is easiest to first find both f(a + h) and f(a). We can then utilize the results to write the desired quotient. h We begin by calculating f(a+h). For that, we substitute a + h for x, expand the parentheses, combine like terms, and simplify. f(x) = 5x²15x + 8 f(a+h) = 5(a + h)² ? 15(a + h) + 8 = 5a² + 10ah +5h² - 15a - 15h + 8 (h = 0) 10ah Next, we determine f(a). Note that no simplification is needed. f(x) = 5x²15x + 8 f(a) 5a² + 8 = I Consider the following functions. f(x) = = 1; g(x) = x² + 8 X-8 Complete the following statement, given that h = (gof). h(9) = g v f v (9)) g ]× ) X || = 9