(Solved): Please help and show work thanks! Submission 1 (1/2 points) Saturday, July 23, 2022 06:01 AM CDT C ...

Please help and show work thanks!

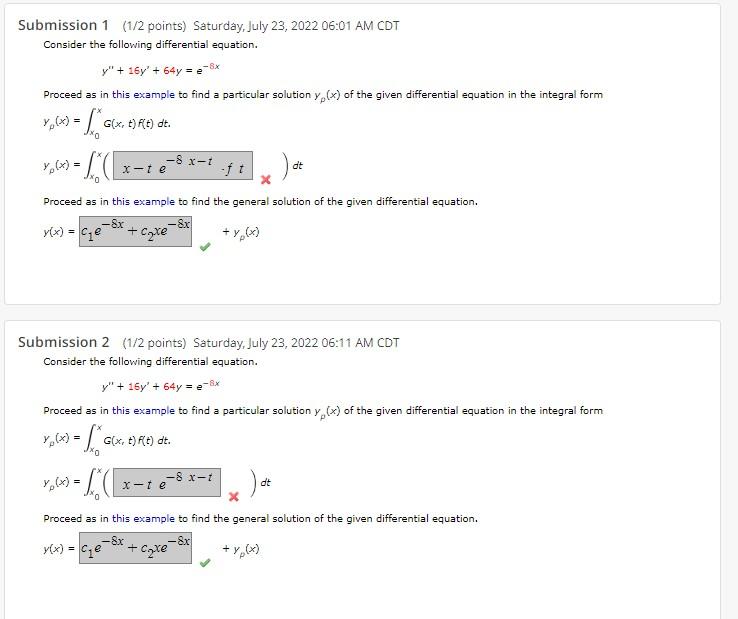
Submission 1 (1/2 points) Saturday, July 23, 2022 06:01 AM CDT Consider the following differential equation. \[ y^{\prime \prime}+16 y^{\prime}+64 y=e^{-8 x} \] Proceed as in this example to find a particular solution \( y_{\rho}(x) \) of the given differential equation in the integral form \[ \begin{array}{l} y_{\rho}(x)=\int_{x_{0}}^{x} G(x, t) f(t) d t . \\ y_{\rho}(x)=\int_{x_{0}}^{x}\left(x-t e^{-8 x-t}-f t x_{x}\right) d t \end{array} \] Proceed as in this example to find the general solution of the given differential equation. \[ y(x)=c_{1} e^{-8 x}+c_{2} x e^{-8 x}+y_{p}(x) \] Submission 2 (1/2 points) Saturday, July 23, 2022 06:11 AM CDT Consider the following differential equation. \[ y^{\prime \prime}+16 y^{\prime}+64 y=e^{-8 x} \] Proceed as in this example to find a particular solution \( y_{\rho}(x) \) of the given differential equation in the integral form \[ \begin{array}{l} y_{\rho}(x)=\int_{x_{0}}^{x} G\left(x_{t}, t\right) f(t) d t . \\ y_{\rho}(x)=\int_{x_{0}}^{x}\left(x_{x}\right) d t \end{array} \] Proceed as in this example to find the general solution of the given differential equation. \[ y(x)=c_{1} e^{-8 x}+c_{2} x e^{-8 x}+y_{p}(x) \]