Home /
Expert Answers /
Calculus /
please-help-i-already-asked-and-chegg-gave-the-wrong-answers-please-help-with-all-three-questions-pa843
(Solved): Please help, I already asked and chegg gave the wrong answers. Please help with all three questions. ...
Please help, I already asked and chegg gave the wrong answers. Please help with all three questions. Thank you
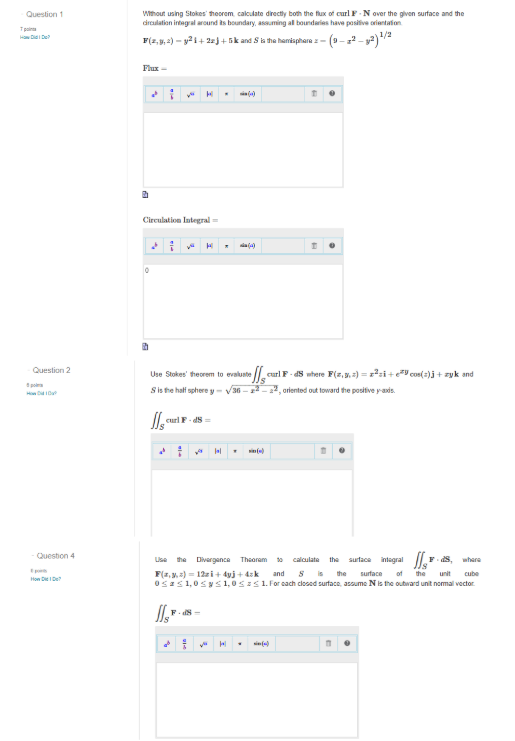
Without using Stokes' theorem, calculate directly both the flux of curl F*N over the given surface and the
circulation integral around its boundary, assuming all boundaries have positive orientation.
F(x,y,z)=y^(2)i+2xj+5k and S is the hemisphere z=(9-x^(2)-y^(2))^((1)/(2))
Flux =
Circulation Integral = Use Stokes' theorem to evaluate ∬_(S)curlF*dS where F(x,y,z)=x^(2)zi+e^(xy)cos(z)j+xyk and
S is the half sphere y=\sqrt(36-x^(2)-z^(2)), oriented out toward the positive y-axis.
∬_(S)curlF*dS= Use the Divergence Theorem to calculate the surface integral ∬_(S)F*dS, where
F(x,y,z)=12\xi +4yj+4zk and S is the surface of the unit cube
0<=x<=1,0<=y<=1,0<=z<=1. For each closed surface, assume N is the outward unit normal vector.
∬_(S)F*dS=Use Stokes' theorem to evaluate ∬_(S)curlF*dS where F(x,y,z)=x^(2)zi+e^(xy)cos(z)j+xyk and
S is the half sphere y=\sqrt(36-x^(2)-z^(2)), oriented out toward the positive y-axis.
∬_(S)curlF*dS=
\table[[a^(b),(a)/(b)]]
\sqrt(\bar (a) )
|a|
\pi
\pi
Whout using Stokes' theorem, calculate drectly both the flux of curl F*N over the given surface and the
circulation integral around is boundary, asouming al bourdaries have pasilive oriestation.
F(x,y,z)=y^(2)i+2xj+5k and S is the hemisphere x-(9-x^(2)-y^(2))^((1)/(2))
Flux -
Circulation Integral =
Use Stokes' theorem to evaluate ∬_(S)curlF*dS where F(z,y,z)=x^(2)zi+e^(xy)cos(z)j+xyk and
S is the hall sphere y-\sqrt(36-x^(2)-2^(2)), ariented out loward the posifive y-axis.
∬_(S)curlF*dS=
Use the Divergence Theorem to calculate the surface integral ∬_(S)F*dS, where
F(x,y,z)=12\xi +4yj+4zk and S is the surface of the unit cube
0<=x<=1,0<=y<=1,0<=z<=1. For each closed surface, asoume N is the outhord unit nomal vector
∬_(S)F*ds=