(Solved): please help! will like asap! If \( X \) is any random variable with expected value \( \mu_{X} \) and ...

If \( X \) is any random variable with expected value \( \mu_{X} \) and variance \( \sigma_{X}^{2} \), and a new random variable \( Z \) is defined from \( X \) by the equation \( Z=a X+b \), then: Rule 1...Z has the expected value \( E(Z) \equiv \mu_{Z}=a \mu_{X}+b ; \) and Rule 2 has \( \quad \) variance \( V(Z) \equiv \operatorname{Var}(Z) \equiv \sigma_{Z}^{2}=a^{2} \sigma_{X}^{2} \) and standard deviation \( \sigma_{Z}=|a| \sigma_{x} \). You should notice that while Rule 1 involves both \( a \) and \( b \), Rule 2 only involves \( a \). In words, if you shift a random variable by adding or subtracting a constant, that will only change the expected value of the random variable, not the variance. The two bars around a constant-like \( |a| \) in the standard deviation expression-means the "absolute value of \( a \)." Search the web for "absolute value" if you've forgotten what that is. Rules 3,4 , and 5 (these replace rules 3,4 , and 5 on pages \( 230-231 \) of the text) If: \( \quad X \) is any random variable with expected value \( \mu_{X} \) and variance \( \sigma_{X}^{2} \); and \( Y \) is any random variable with expected value \( \mu_{Y} \) and variance \( \sigma_{Y}^{2} \); and the covariance of \( X \) and \( Y \) is \( \sigma_{X Y} \); and a new random variable \( Z \) is defined from \( X \) and \( Y \) by the equation \( Z=a X+b Y \), Then: Rule \( 3 \ldots Z \) has the expected value \( E(Z) \equiv \mu_{Z}=a \mu_{X}+b \mu_{Y} \). Rule 4... If we also know that \( X \) and \( Y \) are (statistically) independent random variables, then \( Z \) has the variance \( V(Z) \equiv \operatorname{Var}(Z) \equiv \sigma_{Z}^{2}=a^{2} \sigma_{X}^{2}+b^{2} \sigma_{Y}^{2} \) and standard deviation \( \sigma_{Z}=\sqrt{a^{2} \sigma_{X}^{2}+b^{2} \sigma_{Y}^{2}} \). Rule 5... If we know or suspect that \( X \) and \( Y \) are not independent random variables, then \( Z \) has the variance \( V(Z) \equiv \operatorname{Var}(Z) \equiv \sigma_{Z}^{2}=a^{2} \sigma_{X}^{2}+b^{2} \sigma_{Y}^{2}+2 a b \sigma_{X Y} \) and standard deviation \( \sigma_{Z}=\sqrt{a^{2} \sigma_{X}^{2}+b^{2} \sigma_{Y}^{2}+2 a b \sigma_{X Y}} \). 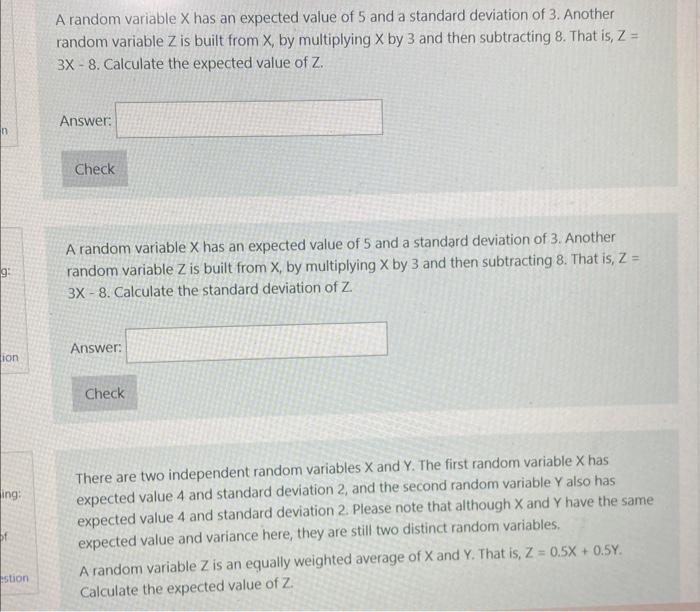A random variable \( \mathrm{X} \) has an expected value of 5 and a standard deviation of 3 . Another random variable \( Z \) is built from \( X \), by multiplying \( X \) by 3 and then subtracting 8 . That is, \( Z= \) \( 3 X-8 \). Calculate the expected value of \( Z \). Answer: A random variable \( X \) has an expected value of 5 and a standard deviation of 3 . Another random variable \( Z \) is built from \( X \), by multiplying \( X \) by 3 and then subtracting 8 . That is, \( Z= \) \( 3 X-8 \). Calculate the standard deviation of \( Z \) Answer: There are two independent random variables \( X \) and \( Y \). The first random variable \( X \) has expected value 4 and standard deviation 2, and the second random variable \( Y \) also has expected value 4 and standard deviation 2. Please note that although \( X \) and \( Y \) have the same expected value and variance here, they are still two distinct random variables. A random variable \( Z \) is an equally weighted average of \( X \) and \( Y \). That is, \( Z=0.5 X+0.5 Y \). Calculate the expected value of \( Z \).