(Solved): please solve problems 5,7,13,19,25,29,31,33,39 and 41 please solve all of them or atleast half ...

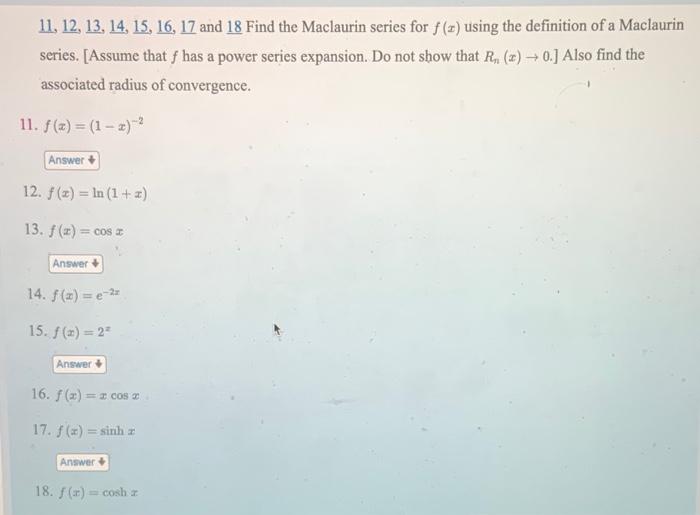
5, 6, 7, 8,2 and 10 Use the definition of a Taylor series to find the first four nonzero terms of the series for \( f(x) \) centered at the given value of \( a \). \[ f(x)=x e^{2}, \quad a=0 \] \[ f(x)=\frac{1}{1+x}, \quad a=2 \] 7. \( f(x)=\sqrt[3]{x}, \quad a=8 \) \( 11,12,13,14,15, \underline{16}, 17 \) and 18 Find the Maclaurin series for \( f(x) \) using the definition of a Maclaurin series. [Assume that \( f \) has a power series expansion. Do not show that \( R_{n}(x) \rightarrow 0 \).] Also find the associated radius of convergence. 11. \( f(x)=(1-x)^{-2} \) 12. \( f(x)=\ln (1+x) \) 13. \( f(x)=\cos x \) 14. \( f(x)=e^{-2 x} \) 15. \( f(x)=2^{2} \) 16. \( f(x)=x \cos x \) 17. \( f(x)=\sinh x \) 18. 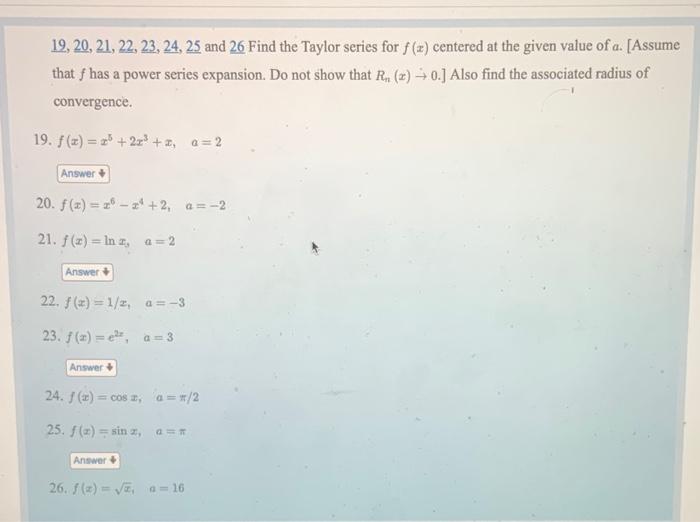\( f(x)=\cosh x \) 19, 20, 21, 22, 23, 24, \( \underline{25} \) and 26 Find the Taylor series for \( f(x) \) centered at the given value of \( a \). [Assume that \( f \) has a power series expansion. Do not show that \( R_{n}(x) \rightarrow 0 \).] Also find the associated radius of convergence. 19. \( f(x)=x^{5}+2 x^{3}+x, \quad a=2 \) 20. \( f(x)=x^{6}-x^{4}+2, \quad a=-2 \) 21. \( f(x)=\ln x_{,} \quad a=2 \) 22, \( f(x)=1 / x, \quad a=-3 \) 23. \( f(x)=e^{2 x}, \quad a=3 \) 24. \( f(x)=\cos x, \quad a=\pi / 2 \) 25. \( f(x)=\sin x, \quad a=\pi \) 26. \( f(x)=\sqrt{x_{1}} \quad a=16 \) \( 31,32,33 \) and 34 Use the binomial series to expand the function as a power series. State the radius of convergence. 31. \( \sqrt[4]{1-x} \) 32. \( \sqrt[3]{8+x} \) 33. \( \frac{1}{(2+x)^{3}} \) 34. \( (1-x)^{3 / 4} \) \( 35,36,37,38,39,40,41,42,43 \) and 44 Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. 35. \( f(x)=\arctan \left(x^{2}\right) \) 36. \( f(x)=\sin (\pi x / 4) \) 37. \( f(x)=x \cos 2 x \) 38. \( f(x)=e^{3 x}-e^{2 x} \) 39. \( f(x)=x \cos \left(\frac{1}{2} x^{2}\right) \) 40. \( f(x)=x^{2} \ln \left(1+x^{2}\right) \) 41. \( f(x)=\frac{x}{\sqrt{4+x^{2}}} \) 42. \( f(x)=\frac{x^{2}}{\sqrt{2+x}} \) 43. \( f(x)=\sin ^{2} x\left[\right. \) Hint: Use \( \sin ^{2} x=\frac{1}{2}(1-\cos 2 x) \), ]