(Solved): Please solve this in details (step by step). Thanks I will rank him high!   1. Consi ...

 

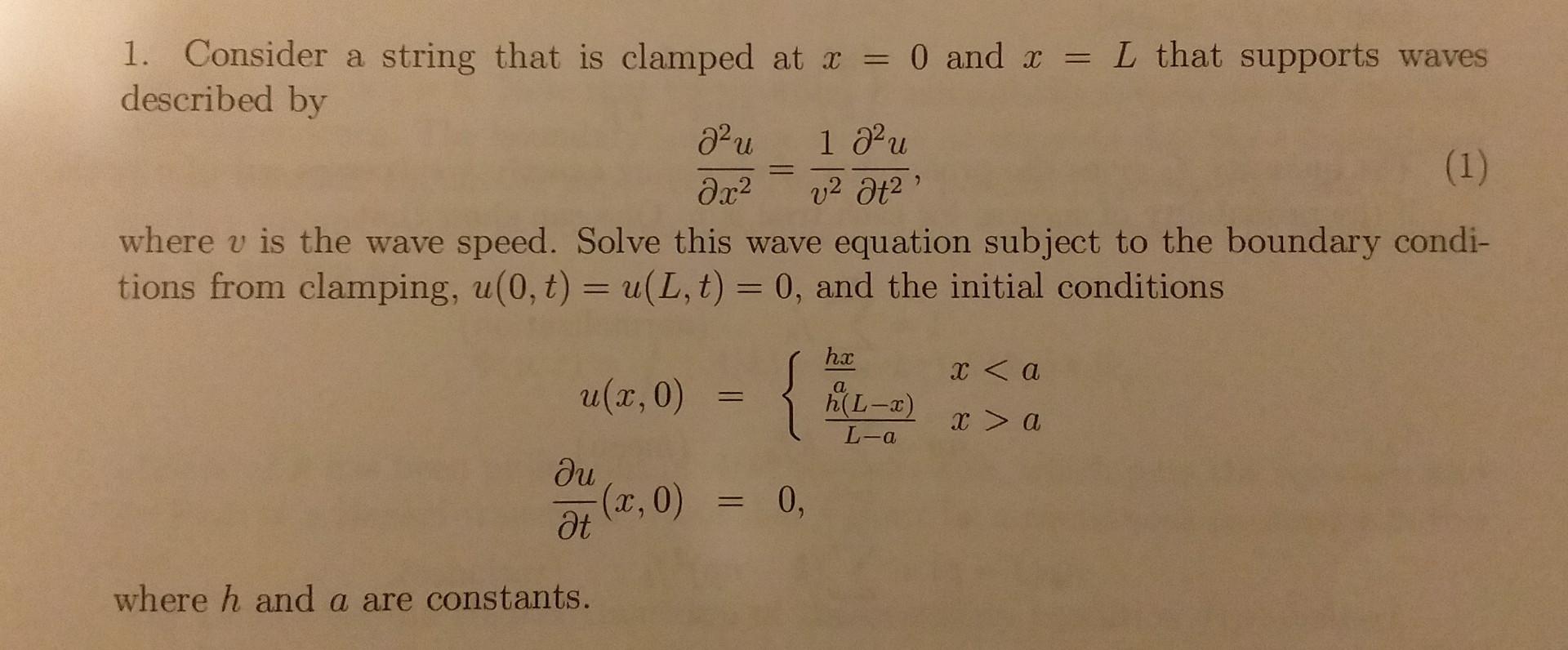
1. Consider a string that is clamped at \( x=0 \) and \( x=L \) that supports waves described by \[ \frac{\partial^{2} u}{\partial x^{2}}=\frac{1}{v^{2}} \frac{\partial^{2} u}{\partial t^{2}}, \] where \( v \) is the wave speed. Solve this wave equation subject to the boundary conditions from clamping, \( u(0, t)=u(L, t)=0 \), and the initial conditions \[ \begin{aligned} u(x, 0) &=\left\{\begin{array}{ll} \frac{h x}{a} & xa \end{array}\right.\\ \frac{\partial u}{\partial t}(x, 0) &=0 \end{aligned} \] where \( h \) and \( a \) are constants.