Home /
Expert Answers /
Calculus /
points-scalc8-4-3-066-let-g-x-int-0-x-f-t-dt-where-f-is-the-function-whose-graph-is-shown-v-pa882
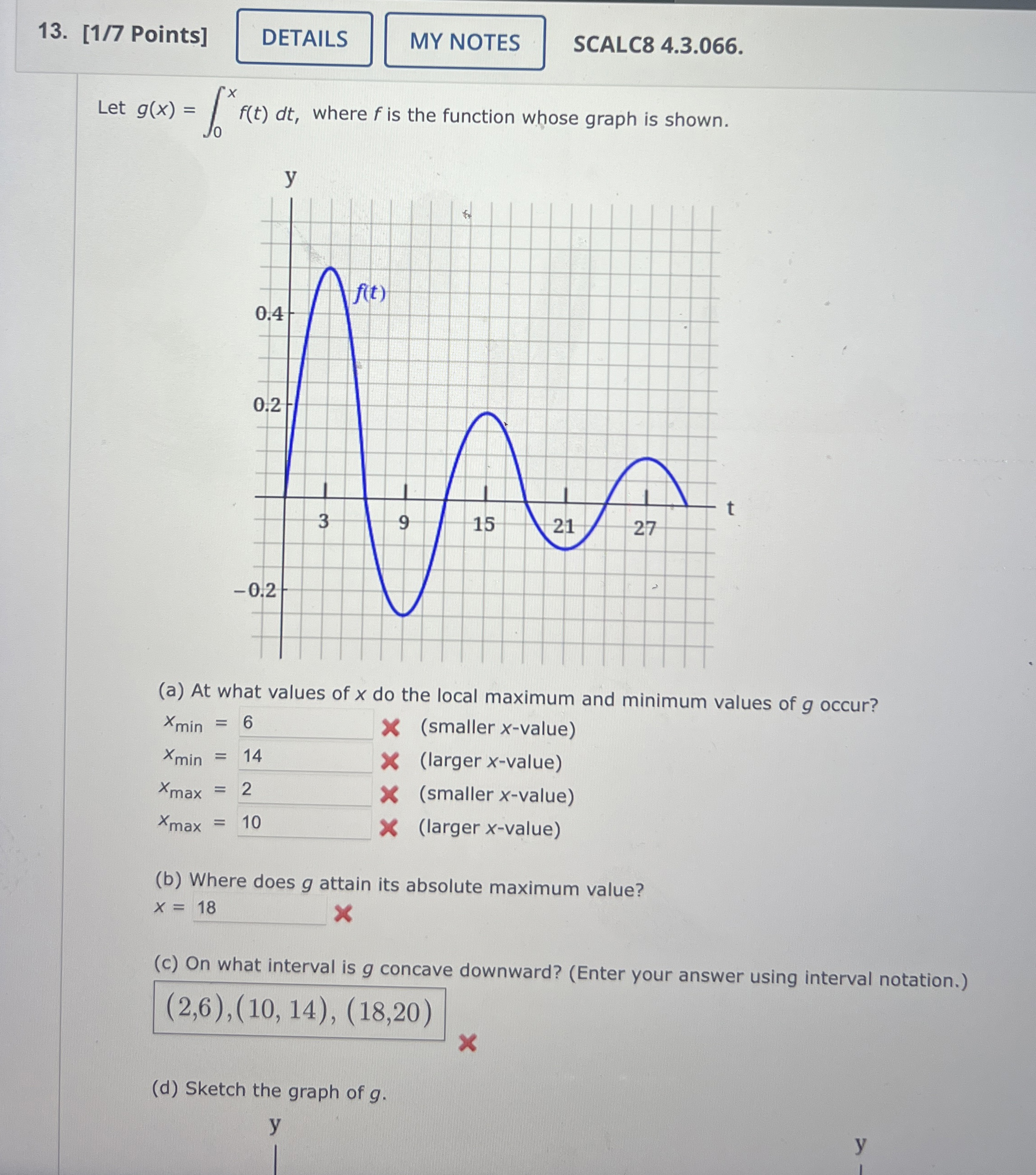
(Solved): Points] SCALC8 4.3.066. Let g(x)=\int_0^x f(t)dt, where f is the function whose graph is shown. v ...
Points] SCALC8 4.3.066. Let
g(x)=\int_0^x f(t)dt, where
fis the function whose graph is shown. v
◻(a) At what values of
xdo the local maximum and minimum values of
goccur?
x_(min)=
◻* (smaller
x-value)
x_(min )=
◻
x(larger
x-value)
x_(max)=
q,X (smaller
x-value)
x_(max)=
◻
x(larger
x-value) (b) Where does
gattain its absolute maximum value?
x=
◻(c) On what interval is
gconcave downward? (Enter your answer using interval notation.)
◻(d) Sketch the graph of
g.
y
y