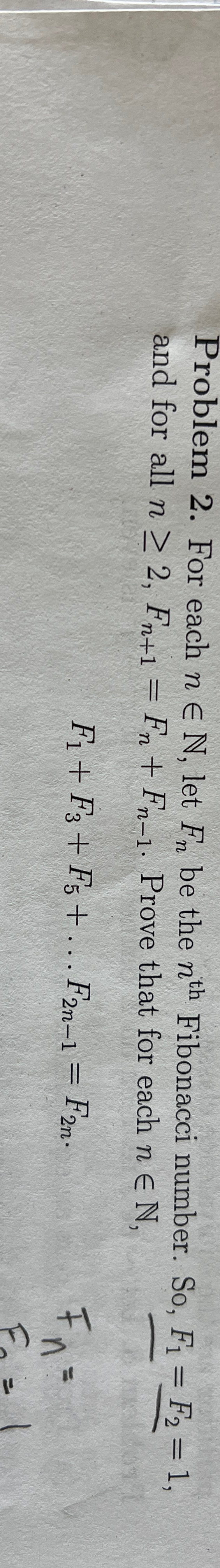Home /
Expert Answers /
Advanced Math /
problem-2-for-each-ninn-let-f-n-be-the-n-th-fibonacci-number-so-f-1-f-2-1-and-for-all-pa709
(Solved): Problem 2. For each ninN, let F_(n) be the n^(th ) Fibonacci number. So, F_(1)=F_(2)=1, and for all ...
Problem 2. For each
ninN, let
F_(n)be the
n^(th )Fibonacci number. So,
F_(1)=F_(2)=1, and for all
n>=2,F_(n+1)=F_(n)+F_(n-1). Prove that for each
ninN,
F_(1)+F_(3)+F_(5)+dotsF_(2n-1)=F_(2n).