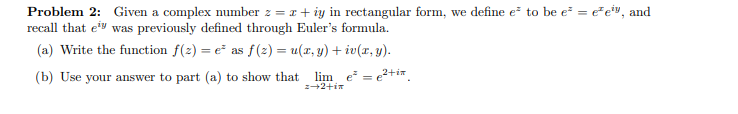Home /
Expert Answers /
Advanced Math /
problem-2-given-a-complex-number-z-x-iy-in-rectangular-form-we-define-e-z-to-be-e-z-e-x-e-pa255
(Solved): Problem 2: Given a complex number z=x+iy in rectangular form, we define e^(z) to be e^(z)=e^(x)e^( ...
Problem 2: Given a complex number
z=x+iyin rectangular form, we define
e^(z)to be
e^(z)=e^(x)e^(iy), and recall that
e^(iy)was previously defined through Euler's formula. (a) Write the function
f(z)=e^(z)as
f(z)=u(x,y)+iv(x,y). (b) Use your answer to part (a) to show that
\lim_(z->2+i\pi )e^(z)=e^(2+i\pi ).