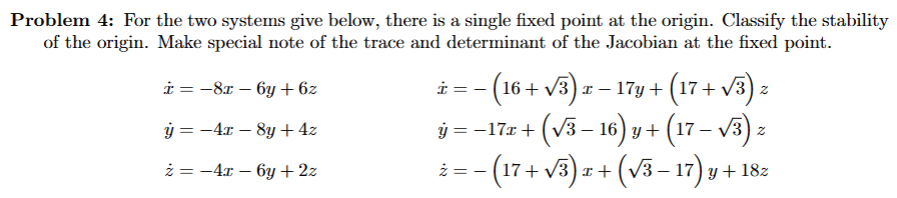Home /
Expert Answers /
Advanced Math /
problem-4-for-the-two-systems-give-below-there-is-a-single-fixed-point-at-the-origin-classify-the-pa378
(Solved): Problem 4: For the two systems give below, there is a single fixed point at the origin. Classify the ...
Problem 4: For the two systems give below, there is a single fixed point at the origin. Classify the stability
of the origin. Make special note of the trace and determinant of the Jacobian at the fixed point.
x^(˙)=-8x-6y+6z
y^(˙)=-4x-8y+4z
z^(˙)=-4x-6y+2z
x^(˙)=-(16+\sqrt(3))x-17y+(17+\sqrt(3))z
y^(˙)=-17x+(\sqrt(3)-16)y+(17-\sqrt(3))z
z^(˙)=-(17+\sqrt(3))x+(\sqrt(3)-17)y+18z