(Solved): problem 5 please 2. (20p) Let \( G \) be a group and \( Z(G):=\{x \in G \mid g x=x g \) for all \( g ...

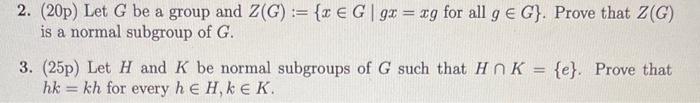
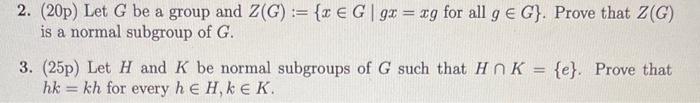
2. (20p) Let \( G \) be a group and \( Z(G):=\{x \in G \mid g x=x g \) for all \( g \in G\} \). Prove that \( Z(G) \) is a normal subgroup of \( G \). 3. (25p) Let \( H \) and \( K \) be normal subgroups of \( G \) such that \( H \cap K=\{e\} \). Prove that \( h k=k h \) for every \( h \in H, k \in K \). 5. (10p) Let \( G \) be a group and let \( Z(G) \) be the center of \( G \) as defined in Problem 2 above. Assume that the factor group \( G / Z(G) \) is cyclic. Prove that \( Z(G)=G \).