(Solved): Problem No. 2: Eight baskets of oranges are to be distributed among 3 stores. The demand for the ora ...

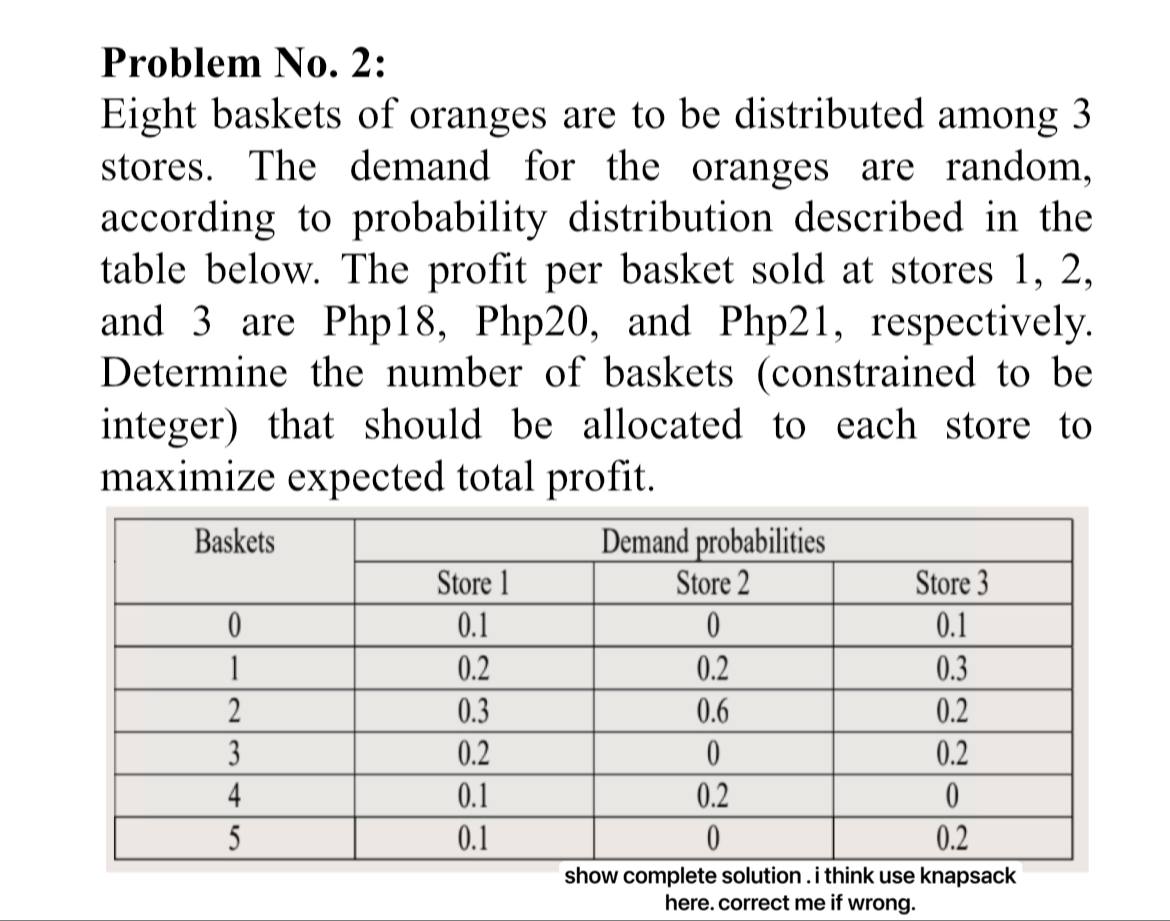
Problem No. 2: Eight baskets of oranges are to be distributed among 3 stores. The demand for the oranges are random, according to probability distribution described in the table below. The profit per basket sold at stores 1, 2, and 3 are \( \mathrm{Php} 18, \mathrm{Php} 20 \), and Php 21 , respectively. Determine the number of baskets (constrained to be integer) that should be allocated to each store to maximize expected total profit. \begin{tabular}{|c|c|c|c|} \hline \multirow{2}{*}{ Baskets } & \multicolumn{3}{|c|}{ Demand probabilities } \\ \cline { 2 - 4 } & Store 1 & Store 2 & Store 3 \\ \hline 0 & 0.1 & 0 & 0.1 \\ \hline 1 & 0.2 & 0.2 & 0.3 \\ \hline 2 & 0.3 & 0.6 & 0.2 \\ \hline 3 & 0.2 & 0 & 0.2 \\ \hline 4 & 0.1 & 0.2 & 0 \\ \hline 5 & 0.1 & 0 & 0.2 \\ \hline \end{tabular} show complete solution .i think use knapsack here. correct me if wrong.