(Solved): Prove that 4ex is equal to the sum of its Maclaurin series. Solution If f(x)=4ex, then f(n+1)(x)= f ...

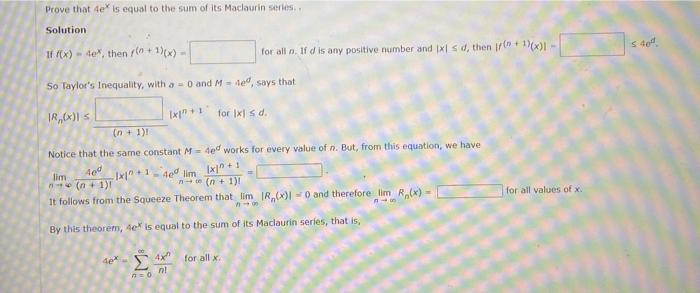
Prove that $4e^x$ is equal to the sum of its Maclaurin series. Solution If $f(x)=4e^x$, then $f^{(n+1)}(x)=$ for all $n$. If $d$ is any positive number and $|x|\le d,then\left|f^{(n+1)}(x)\right|=$ So Taylor's Inequality, with $a=0$ and $M=4e^d$, says that $\left|R_n(x)\right|\le \frac{|x{|}^{n+1}}{(n+1)!}\text{ for }|x|\le d\text{. }$ Notice that the same constant $M=4e^d$ works for every value of $n$. But, from this equation, we have ${\lim }_{n\to \infty }\frac{-4e^d}{(n+1)!}|x{|}^{n+1}=4e^d{\lim }_{n\to \infty }\frac{|x{|}^{n+1}}{(n+1)!}=$ It follows from the Squeeze Theorem that ${\lim }_{n\to \infty }\left|R_n(x)\right|=0$ and therefore ${\lim }_{n\to \infty }{R}_n(x)=$ for ail values of $x$. By this theorem, Ae $e^x$ is equal to the sum of its Maclaurin series, that is, $4e^x={\sum }_{n=0}^{\infty }\frac{4x^n}{n!}\text{ for all }x\text{. }$