Home /
Expert Answers /
Geometry /
question-4-the-circle-with-midpoint-m-2-2-is-inscribed-in-abo-ab-is-a-tangent-to-the-pa953
(Solved): QUESTION 4 The circle with midpoint M(-2,2) is inscribed in ()/(_(()/())ABO.AB) is a tangent to the ...
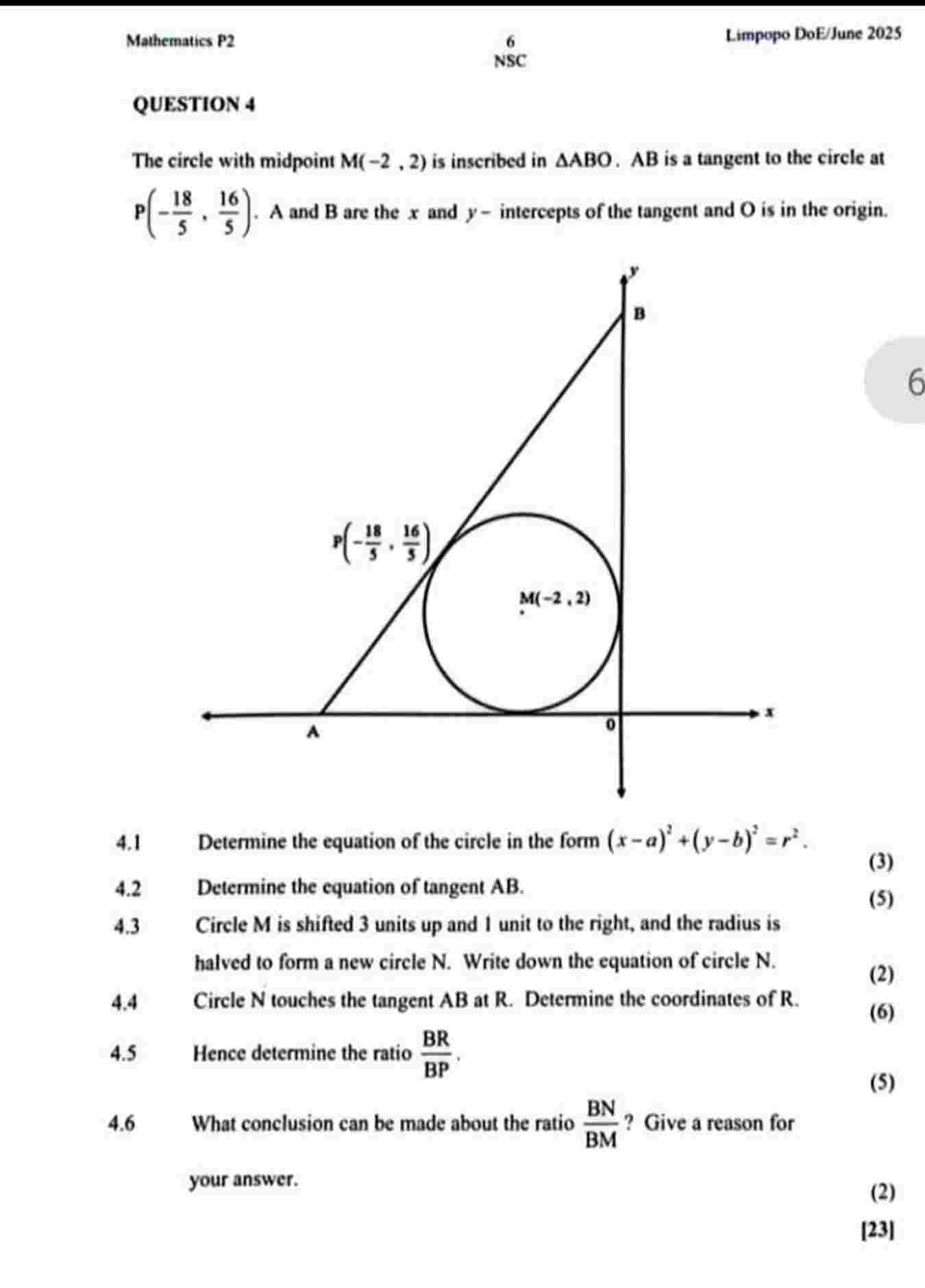
QUESTION 4
The circle with midpoint M(-2,2) is inscribed in ()/(_(()/())ABO.AB) is a tangent to the circle at
P(-(18)/(5),(16)/(5)).A and B are the x and y - intercepts of the tangent and O is in the origin.
4.1 Determine the equation of the circle in the form (x-a)^(2)+(y-b)^(2)=r^(2).
4.2 Determine the equation of tangent AB .
4.3 Circle M is shifted 3 units up and I unit to the right, and the radius is
halved to form a new circle N . Write down the equation of circle N .
4.4 Circle N touches the tangent AB at R. Determine the coordinates of R.
4.5 Hence determine the ratio (BR)/(BP),
4.6 What conclusion can be made about the ratio (BN)/(BM) ? Give a reason for
your answer.