Home /
Expert Answers /
Advanced Math /
recall-that-the-conjugate-of-the-complex-number-z-a-b-i-is-defined-to-be-bar-z-a-b-i-pa256
(Solved): Recall that the conjugate of the complex number \( z=a+b i \) is defined to be \( \bar{z}=a-b i \). ...
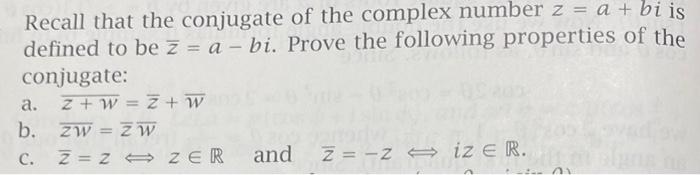
Recall that the conjugate of the complex number \( z=a+b i \) is defined to be \( \bar{z}=a-b i \). Prove the following properties of the conjugate: a. \( \overline{z+w}=\bar{z}+\bar{w} \) b. \( \overline{z w}=\bar{z} \bar{w} \) c. \( \bar{z}=z \Leftrightarrow z \in \mathbb{R} \) and \( \bar{z}=-z \Leftrightarrow i z \in \mathbb{R} \).
Expert Answer
Given, conjugate of a complex number z=a+bi is defined to be z?=a?ib a) Let z=a+ib,w=x+iy Then, z+w?=(a+ib)+(x+iy)? = (a+x)+i(b+y)? = (a+x)?i(b+y) {by