(Solved): Seepage exists in the soil profile in Figure a. Thickness of the dry sand and saturated sand layers ...

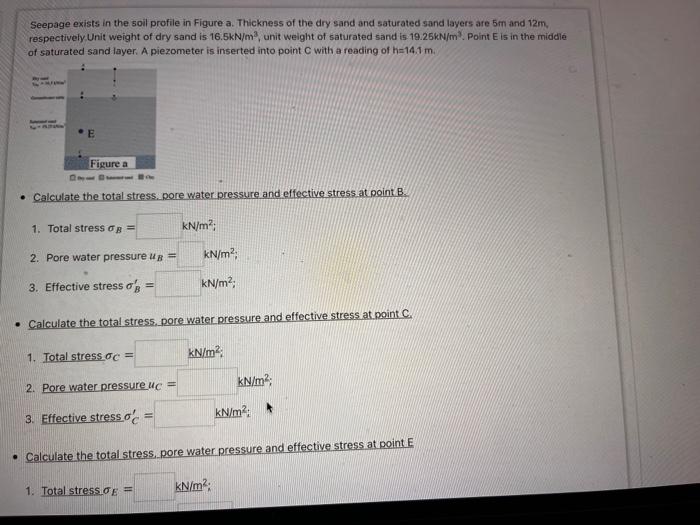
Seepage exists in the soil profile in Figure a. Thickness of the dry sand and saturated sand layers are \( 5 \mathrm{~m} \) and \( 12 \mathrm{~m} \), respectively Unit weight of dry sand is \( 16.5 \mathrm{kN} / \mathrm{m}^{3} \), unit weight of saturated sand is \( 19.25 \mathrm{kN} / \mathrm{m}^{2} \). Point \( E \) is in the middie of saturated sand layer. A piezometer is inserted into point \( \mathrm{C} \) with a reading of \( \mathrm{h}=14.1 \mathrm{~m} \). - Calculate the total stress. pore water pressure and effective stress at point B. 1. Total stress \( \sigma_{B}= \) \( k N / m^{2} \) 2. Pore water pressure \( u_{B}=\quad \mathrm{kN} / \mathrm{m}^{2} \), 3. Effective stress \( \sigma_{B}^{\prime}=\quad \quad \mathrm{kN} / \mathrm{m}^{2} \); - Calculate the total stress, pore water pressure and effective stress at point C. 1. Total stress \( \sigma_{C}= \) 2. Pore water pressure \( u_{C}= \) \( \mathrm{kN} / \mathrm{m}^{2} \) 3. Effective stress \( \sigma_{C}^{\prime}= \) \( \mathrm{kN} / \mathrm{m}^{2}+ \) Calculate the total stress, pore water pressure and effective stress at point E 1. 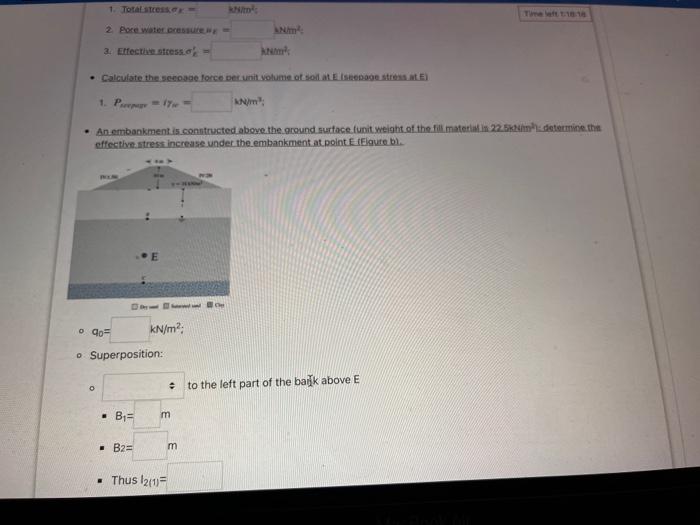Total stress \( \sigma_{E}=\quad \mathrm{kN} / \mathrm{m}^{2} \); 3. Gifection thessof \( = \) - An-embankment is conntructed aboye the ground surtace fumit weight of the fill inatet if cffective strest increase under the embankment at polnt E fEigute b). 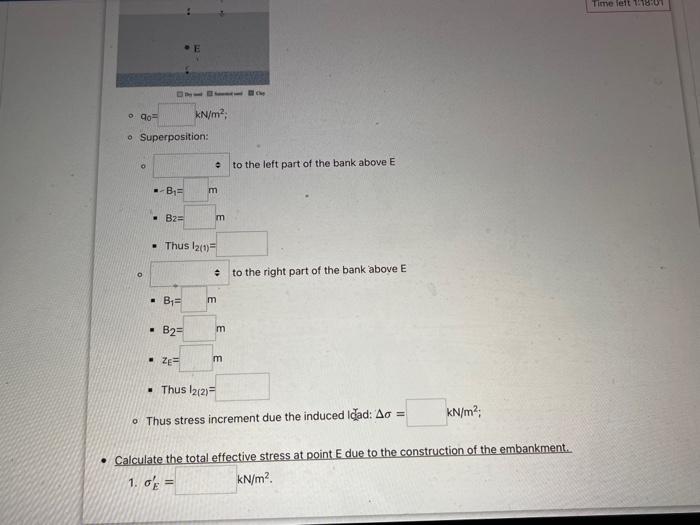- \( 9_{0}= \) - Superposition: \( 9_{0}=\mathrm{kN} / \mathrm{m}^{2} \) - Superposition: - to the left part of the bank above \( E \) - Thus \( I_{2(1)}= \) . to the right part of the bank above \( E \) \( -\mathrm{B}_{1}=\quad m \) \( -B_{2}=m \) - \( z_{E}=m \) - Thus \( \mathrm{I}_{2(2)}= \) - Thus stress increment due the induced ld?ad: \( \Delta \sigma= \) Calculate the total effective stress at point E due to the construction of the embankment. 1. \( \sigma_{E}^{\prime}=\mathrm{kN} / \mathrm{m}^{2} \).