Home /
Expert Answers /
Mechanical Engineering /
show-all-work-step-by-step-3-for-the-mechanical-system-shown-below-find-a-state-variable-representa-pa835
Expert Answer
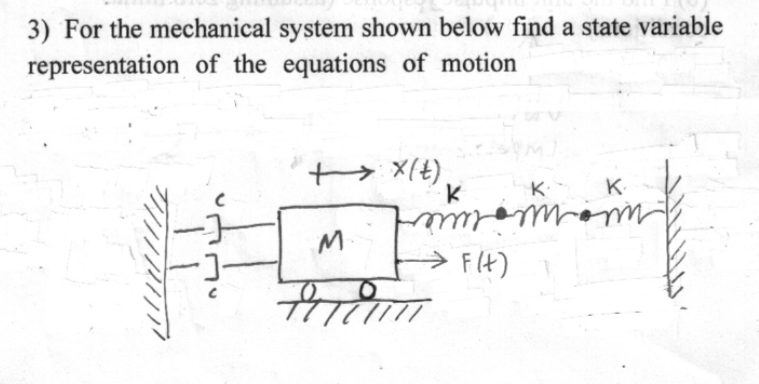
==>To find the state variable representation of the given mechanical system, we need to derive the equations of motion based on the given diagram. From the diagram, it seems that we have a mass-spring-damper system with an external force.Let's denote the state variables as follows:x? = position of the mass (displacement)x? = velocity of the massThe equation of motion for the mass can be written as: Where:m = mass of the systemk?, k? = spring constantsc = damping coefficientF(t) = external forceTo convert this second-order differential equation into a set of first-order differential equations, we introduce two new state variables: (velocity) (acceleration)Now, we can rewrite the equation of motion as a system of first-order differential equations: Finally, the state variable representation of the system is given by: